Напряженность электрического поля

Сложение электрических полей (принцип суперпозиции)

Распределение зарядов

Линии напряженности электрического поля

Теорема Гаусса для поля в вакууме

Поле равномерно заряженной сферической поверхности

Поле объемно заряженного шара

Поле равномерно заряженной бесконечной плоскости

Поле равномерно заряженного бесконечного цилиндра (нити)

Циркуляция вектора напряженности электростатического поля

 

Взаимодействие между покоящимися зарядами осуществляется через электрическое поле.

Если все заряды, создающие поле, в данной системе отсчета неподвижны, то поле называется электростатическим.

Электрическое поле – векторное поле, определяющее воздействие на заряженные частицы, не зависящее от их скоростей. Электрическое поле является одной из компонент единого электромагнитного поля.

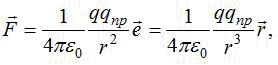(1.3)

здесь   - единичный вектор, направленный от заряда q к пробному заряду q_пр,  - радиус-вектор, направленный от заряда в данную точку поля, определяющий положение пробного заряда q_пр относительно заряда q.

Отношение   для пробного заряда любой величины будет одним и тем же и зависит только от величины заряда q и . Поэтому это отношение принято в качестве величины, характеризующей электрическое поле.

Напряженностью электрического поля в данной точке называется отношение силы, действующей со стороны электрического поля на покоящийся пробный заряд

(1.4)

Единица измерения в СИ: 1Н/Кл = 1 В/м.

Напряженность численно равна силе, действующей со стороны электрического поля на единичный положительный заряд, помещенный в данную точку поля.                                                                                          

Напряженность точечного заряда в вакууме

(1.5)

где  – радиус-вектор, направленный от заряда в данную точку поля, а r – модуль этого вектора.

Рис. 1.3. Направление напряженности электрического поля, создаваемого положительным (а) и отрицательным (б) зарядами

Направление этого вектора определяет направление силы, действующей на положительный заряд, помещенный в рассматриваемую точку поля (рис. 1.3).

Если известна напряженность поля в какой-либо точке, то тем самым определена и сила, действующая на электрический заряд, помещенный в эту точку:

(1.6)

Напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:

(1.7)

Рис. 1.4. Сложение электрических полей

В качестве примера рассмотрим поле двух точечных зарядов q₁ и q₂ (рис. 1.4).  – напряженность поля в точке а, создаваемая зарядом q₁, а  – напряженность поля заряда q₂. – напряженность результирующего поля.

Если заряженное тело настолько велико, что его нельзя рассматривать как точечный заряд, то в этом случае необходимо знать распределение зарядов внутри тела, пространственное расположение зарядов принято описывать с помощью: объемной плотности заряда (r), поверхностной плотности заряда (s) и линейной плотности заряда (l). Эти величины определяются формулами:

объемная плотность заряда r		(1.8 a)
поверхностная плотность заряда s		(1.8 б)
линейная плотность заряда l		(1.8 в)

где dq – заряд, заключенный соответственно в объеме dV, на поверхности dS  и на длине dl.

При непрерывном распределении зарядов

(1.9)

Например, если заряд распределен по объему с плотностью r, то формула (1.9) примет вид       

(1.9а)

где интегрирование проводят по всему пространству, в котором r отлично от нуля.

Рис. 1.5. К определению линий напряженности

Электрическое поле можно представить с помощью линий напряженности (силовых линий). Эти линии проводят так, чтобы касательная к ним в каждой точке совпадала с направлением вектора , а густота линий, т.е. число линий, пронизывающих единичную площадку, перпендикулярную линиям в данной точке, была бы пропорциональна модулю вектора  (рис. 1.5).

Рис. 1.6. Линии напряженности точечного заряда

На рис. 1.6 показана картина линий напряженности точечного заряда. Густота линий напряженности на каком-либо расстоянии r от заряда равна отношению полного числа N линий напряженности, вышедших из заряда, к поверхности сферы  радиуса  r, т.е. N/(4pr2). Она убывает обратно пропорционально квадрату расстояния от заряда, т.е. так же, как и напряженность поля. На рис. 1.7 показано электрическое поле между двумя одинаковыми шариками, заряженными разноименно.

Рис. 1.7. Линии напряженности электрического поля двух разноименных зарядов

Рис. 1.8. Электрическое поле плоского конденсатора

Если вектор напряженности в любой точке поля постоянен по модулю и направлению, то такое поле называется однородным. Таким полем является, например, электрическое поле между двумя параллельными металлическими пластинами, заряженными разноименными зарядами (плоский конденсатор), если расстояние между пластинами мало по сравнению с размерами пластин (рис. 1.8).

Основной задачей электростатики является вычисление полей заряженных тел. Найти напряженность поля заряженного тела можно с помощью:

1) принципа суперпозиции - это сложная математическая задача, решаемая только в некоторых простых случаях;

2) теоремы Гаусса, которая упрощает расчеты, но только в случае бесконечной плоскости, бесконечной нити (цилиндра) или сфер и шаров (см. ниже).

Сначала введем понятие «поток вектора» - это скалярная величина.

Рис. 1.9. Поток вектора напряженности через поверхность dS	Поток вектора напряженности dФ равен числу силовых линий, пронизывающих элементарную площадку dS, нормаль которой составляет угол a с вектором . Согласно рис. 1.9 dФ определяется как
		(1.10)
	где En  – проекция вектора  на нормаль  к площадке dS; – вектор, модуль которого равен dS, направление совпадает с нормалью  к площадке.

Поток вектора  сквозь произвольную замкнутую площадку S:

(1.11)

Теорема Гаусса.

Поток  Ф   вектора      сквозь произвольную замкнутую поверхность S равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на e₀:

(1.12)

Если заряд распределен в пространстве с объемной плотностью r, то теорема Гаусса для электрического поля в вакууме:

(1.12а)

Рассмотрим некоторые простые примеры вычисления электрического поля с помощью теоремы Гаусса. Чтобы найти напряженность с помощью теоремы Гаусса, нужно взять интеграл. Надо суметь выбрать такую замкнутую поверхность, в каждой точке которой было бы Е = const, и cosa = const. Тогда в левой части теоремы Е и cosa можно будет вынести из-под знака интеграла. Поэтому практически теорему Гаусса можно применить только в следующих случаях: сфера, шар, длинная нить, длинный цилиндр, бесконечная плоскость.

1. Поле равномерно заряженной сферической поверхности

Рис. 1.10. Электрическое поле заряженной   сферы

Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью s. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис. 1.10, а). Напряженность поля будет, таким образом, одинакова во всех точках воображаемой сферы радиуса r, концентричной с заряженной сферой. Поскольку напряженность поля  перпендикулярна поверхности, теорема Гаусса дает

или .

Если r < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности Е = 0. График зависимости Е от r приведен на рис. 1.10, б.

2. Поле объемно заряженного шара

Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью r.

Учитывая соображения симметрии, при r ³ R получим, как и в случае сферической поверхности:

(r ³ R).

Рис. 1.11. Зависимость напряженности поля равномерно заряженного шара от расстояния r	Внутри шара при r¢ < R, Q¢ = 4/3 p r¢ 3r. Поэтому, согласно теореме Гаусса
	Учитывая, что r =Q/(4/3 p R3), получим
	,	(r £  R).
	График зависимости E от r приведен на рис. 1.11.

3. Поле равномерно заряженной бесконечной плоскости

Рис.1.12. Электрическое поле равномерно заряженной плоскости

Бесконечная плоскость заряжена с постоянной плотностью +s. Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Поскольку через боковую поверхность цилиндра поток равен нулю, весь поток проходит сквозь его основания (рис. 1.12 а). По теореме Гаусса   Отсюда напряженность электрического поля равна . График зависимости E от r приведен на рис. 1.12 б.

4. Поле равномерно заряженного бесконечного цилиндра (нити)

Рис. 1.13. Электрическое поле равномерно заряженного цилиндра

Бесконечный цилиндр радиуса R заряжен равномерно; линейная плотность заряда равна l. Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l (рис. 1.13 а). Поскольку вектор напряженности параллелен торцам, поток сквозь основания цилиндра равен нулю, и .   Отсюда при r ³ R .   Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0. График зависимости E от r приведен на рис. 1.13 б.

Интеграл по замкнутому пути  называют циркуляцией вектора напряженности.

Циркуляция вектора напряженности электрического поля вдоль любого контура равна нулю. Это утверждение называют теоремой о циркуляции вектора .

(1.13)

Силовое поле, обладающее свойством (1.15), называют потенциальным.

Теорема о циркуляции вектора напряженности позволяет сделать вывод, что в электростатическом поле замкнутых линий вектора напряженности не существует: линии начинаются на положительных зарядах и кончаются на отрицательных (или уходят в бесконечность).