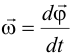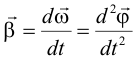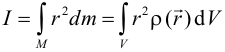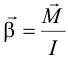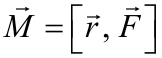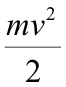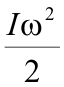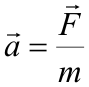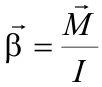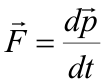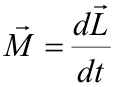LR 1

111

Лабораторная работа № 1. Маятник Обербека
(изучение динамики вращательного движения)

Цель работы: экспериментальная проверка основного закона вращательного движения.

Оборудование, средства измерения: маятник Обербека, набор грузов, секундомер, линейка.

Краткая теория

Вращательным движением твердого тела называется такое движение, при котором траектории всех точек твердого тела представляют собой концентрические окружности с центрами на одной прямой, называемой осью вращения (рис. 1). При этом положение тела в любой момент времени определяется углом поворота φ.

Рис. 1. Вращение твердого тела.

Вращение твердого тела характеризуется угловой скоростью ω:

и угловым ускорением β:

Вектор ω направлен вдоль оси вращения, так же как и вектор dφ, направление их определяется по правилу правого винта. Вектор β направлен вдоль оси вращения в сторону вектора приращения угловой скорости. Линейная скорость точки v связана с угловой скоростью и радиусом траектории соотношением

Связь линейного ускорения точки с угловым ускорением:

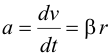При равномерном вращении

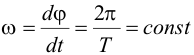где Т – период вращения.

Вращательное движение составляет, в частности, основу движений элементов опорно-двигательного аппарата человека и животных.

Вращательное движение твердого тела совершается под действием сил, лежащих в плоскостях, перпендикулярных к оси вращения, и не проходящих через ось вращения. Мерой взаимодействия тел при вращательном движении является не сила, как при поступательном движении, а момент силы M. Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиус-вектора r, проведенного из точки О в точку А приложения силы F (рис. 2):

Рис. 2. К определению момента силы.

Модуль момента силы

где l = r sin α – плечо силы – кратчайшее расстояние между линией действия силы и точкой О; α – угол между векторами r и F. Свойства векторного произведения описаны в Приложении.

Инертность тел при поступательном движении учитывается с помощью массы m. При вращательном движении мерой инертности служит другая величина – момент инерции тела I. Момент инерции материальной точки равен произведению массы m на квадрат расстояния до оси вращения r

Момент инерции – величина аддитивная: момент инерции всего тела равен сумме моментов инерции его отдельных частей. Поэтому момент инерции системы материальных точек относительно оси вращения

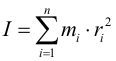где m_i – масса i-й точки до оси вращения; r_i – расстояние i-й точки до оси вращения.

В случае непрерывного распределения масс (твердого тела), тело можно представить в виде совокупности множества малых элементов (рис. 3), тогда приближенное значение I можно найти с помощью вышеприведенной формулы, т.е. проводя суммирование по всем элементам. При измельчении разбиения точность вычисления повышается и, переходя к бесконечно большому числу элементов, получаем интеграл:

где интегрирование производится по всей массе или объему твердого тела. Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

Рис. 3. Разбиение твердого тела на отдельные элементарные части для нахождения момента инерции .

Если ось вращения не проходит через центр масс тела, то используют теорему Штейнера:

где I₀ – момент инерции относительно оси, проходящей через центр масс и параллельной оси вращения; m – масса тела; d – расстояние между осями.

Опыт показывает, что при вращательном движении

– это основное уравнение динамики вращательного движения (2-й закон Ньютона для вращательного движения). Именно его и необходимо проверить в данной работе.

В обобщенном виде второй закон Ньютона для вращательного движения запишется в виде

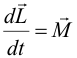где L – момент импульса твердого тела:

Внимание! Математическая форма записи основных закономерностей для поступательного и вращательного движений остается неизменной.

Сравните!

Поступательное движение		Вращательное движение
Масса	m	Момент инерции	I
Перемещение		Угловое перемещение
Скорость		Угловая скорость
Ускорение		Угловое ускорение
Сила		Момент силы
Импульс		Момент импульса
Работа		Работа
Кинетическая энергия		Кинетическая энергия
Основное уравнение динамики		Основное уравнение динамики
Основное уравнение динамики		Основное уравнение динамики

Описание экспериментальной установки

Работа выполняется с помощью маятника Обербека (рис. 4). Вращающаяся часть установки состоит из четырех спиц, укрепленных на втулке под прямым углом друг к другу. На ось втулки насажены два легких шкива различных радиусов r₁ = 9,3 мм и r₂ = 17,5 мм. Вращение происходит вокруг горизонтальной оси. Момент инерции системы относительно оси вращения можно изменить либо изменяя массы грузиков, укрепленных на спицах, либо перемещая грузики вдоль спиц.

Рис. 4. Маятник Обербека.

Каждый раз, закрепляя грузики на спицах на определенном расстоянии от оси вращения, необходимо проверить, правильно ли сбалансирована система, т. е. находится ли она в безразличном равновесии.

Момент силы, вызывающий вращение маятника, создается натяжением нити, навитой на один из шкивов установки, к которой привязан груз m. Момент силы можно изменять, подвешивая к нити грузы различной массы или изменяя плечо силы, для чего нить закрепляется на шкивах разного диаметра.

Под действием груза нить разматывается и приводит во вращение крестовину маятника. Измеряя время t, в течение которого груз m из состояния покоя опустится на расстояние h, можно определить линейное ускорение:

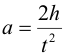Зная радиус шкива можно найти угловое ускорение:

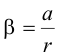Если через Т обозначить силу натяжения нити, то во время равноускоренного падения груза ее величина будет равна:

Следовательно, вращающий момент относительно оси вращения установки будет:

Моментом сил трения пренебрегаем.

Задача. Вам необходимо экспериментально установить характер зависимости углового ускорения вращения маятника β от

а) момента силы М (М₁, М₂, М₃),

б) момента инерции I (I ₁, I ₂, I ₃),

Ожидаемые результаты представлены на рис. 5.

Рис. 5. Теоретические зависимости измеряемых величин.

Выполнение опыта

1. Установите грузы на спицах на одинаковых расстояниях от оси вращения. Оставляя неизменным момент инерции системы I = сonst, определите значения угловых ускорений при трех различных значениях вращающего момента, изменяя массу грузов m, подвешенных к нити. Результаты эксперимента занесите в таблицу и затем представьте в виде графика β = f(M). Пользуясь этим графиком, определите момент инерции системы.

2. Повторите весь эксперимент не менее чем для трех различных значений моментов инерции системы и результаты нанесите на тот же график.

3. Пользуясь построенным графиком, определите для одного из значений вращающего момента величину угловых ускорений при различных моментах инерции маятника. Полученные результаты представьте в виде графика, откладывая по оси абсцисс величину момента инерции, а по оси ординат – угловое ускорение β = f(I). Сделайте вывод.

4. Укажите возможные причины ошибок эксперимента.

Положение грузов на спицах	m, кг	t, с	a, м/с²	T, Н	M, Н×м	β, с^-2	I, кг×м²
	m₁ = ... m₂ = ... m₃ = ...
	m₁ = ... m₂ = ... m₃ = ...
	m₁ = ... m₂ = ... m₃ = ...

Контрольные вопросы

Дайте определение физических величин, необходимых для описания вращательного движения тел (углового перемещения, угловой скорости, углового ускорения, момента силы, момента инерции тела, момента импульса). При ответе укажите единицы измерения данных величин в системе СИ.
Что называется моментом силы относительно неподвижной точки? относительно неподвижной оси? Как определяется направление момента силы?
Как определяется момент инерции материальной точки? Системы точек? Твердого тела?
Какова роль момента инерции во вращательном движении?
Что общего, и каково различие в понятиях «масса» и «момент инерции»?
Как можно определить момент инерции тела относительно произвольной оси, если известен момент инерции его относительно оси симметрии, параллельной произвольной оси?
Сравните по величине моменты инерции цилиндрической оболочки и сплошного цилиндра одинаковой массы и радиуса.
Два тела – пустотелый шар и сплошной шар, одинаковых по массе и размерам, – заставили катиться вверх по наклонной плоскости с одинаковыми начальными скоростями. Какое из тел поднимется на большую высоту?
Что такое момент импульса материальной точки? твердого тела? Как определяется направление момента импульса?
Сформулируйте 2-й закон Ньютона для поступательного и вращательного движений.
Объясните, как получена формула .
В чем заключается физическая сущность закона сохранения момента импульса? В каких системах он выполняется? Приведите примеры.
Каким свойством симметрии пространства обусловливается справедливость закона сохранения момента импульса?
Сопоставьте основные уравнения динамики поступательного и вращательного движений, прокомментировав их аналогию.
Какова формула для кинетической энергии тела, вращающегося вокруг неподвижной оси, и как ее вывести?

Задачи

Сила, приложенная к частице, имеет вид (Н). Чему равен момент этой силы M_z относительно оси z, если точка приложения силы имеет координаты (4,2; 6,8; 0) (м).
Частица с радиус-вектором (м), имеет импульс (кг·м/с). Определить: а) момент импульса L частицы относительно точки О; б) моменты импульса L_x, L_y и L_z относительно осей x,y,z.

Чему равен момент инерции I тонкого кольца массы m и радиуса R относительно оси ОО’, проходящей через центр кольца и относительно оси AA’, проходящей через одну из точек кольца?

Обе оси перпендикулярны плоскости кольца (см. рисунок).

Найти момент инерции тонкого однородного стержня относительно оси, перпендикулярной к стержню и проходящей через его конец, если масса стержня m и его длина l.
Найти момент инерции однородного круглого прямого цилиндра массы т и радиуса R относительно оси цилиндра.
Вычислить момент инерции медного однородного диска относительно оси симметрии, перпендикулярной к плоскости диска, если его толщина h и радиус R.
Определите момент инерции I молекулы N₂, если межъядерное расстояние d = 110 пм.
Определите момент инерции молекулы HF, если межъядерное расстояние d = 91,7 пм.
Определите момент инерции молекулы NO, если межъядерное расстояние d = 115 пм.

Рекомендуемая литература

Савельев И.В. Курс общей физики. Т. 1. – М.: Наука, 1986-1988.
Макаров Е.Ф. Озеров Р.П. Физика для химико-технологических специальностей. – М.: Научный мир, 2002. – 624 с.
Джанколи Д. Физика. В 2-х тт., Т.1. – М.: Мир, 1989.
Трофимова Т.И. Курс физики. – М.: Высшая школа, 1990.
Фриш С.Э., Тиморева А.В. Курс общей физики. Т. 1,2. – М.: Гос. изд. физ.-мат. лит., 1961.