На главную
111       111
Лабораторная работа № 4
Исследование колебаний физического маятника
 
Цель работы: исследовать движение физического маятника, определить ускорение свободного падения с помощью физического маятника.
 
Оборудование, средства измерения: маятник с перемещаемым грузом, секундомер.
 
Краткая теория
 
      Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Колебательные процессы широко распространены в технике и окружающем мире. Колебания совершают камертон, груз на конце пружины, колесико балансира в часах, маятник, струны музыкальных инструментов и т.д.
       Механические колебания могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными. Простейшим видом колебательного процесса являются гармонические колебания, которые описываются уравнением
     
Здесь x – смещение тела от положения равновесия, А – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний, t – время. Величина, стоящая под знаком косинуса или синуса, φ = ωt + φ0, называется фазой гармонического колебания. При t = 0 получаем φ = φ0, поэтому φ0 называют начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Физическая величина, обратная периоду колебаний, называется частотой колебаний:
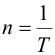Частота колебаний n показывает, сколько колебаний совершается за 1 с. Единица частоты – герц (Гц). Частота колебаний n связана с циклической частотой ω и периодом колебаний T соотношениями:
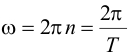      В качестве простейшего примера колебательной системы рассмотрим математический маятник. Математическим маятником называется материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение под действием силы тяжести. Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара (рис. 1).
Рис. 1. Колебания математического маятника.
 
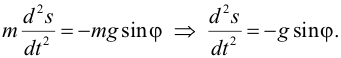Колебания происходят по действием силы F, являющейcя равнодействующей сил тяжести mg и силы натяжения нити T. Как видно из рис. 1, F = mgsinφ. В процессе колебаний шар движется по дуге окружности радиуса l, его положение задается углом φ или длиной дуги s = lφ. Применяя 2-й закон Ньютона , получаем уравнение движения маятника:
или
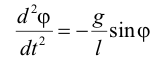Знак минус в правой части выражения учитывает тот факт, что сила F  стремится вернуть маятник в положение равновесия, то есть уменьшить угол отклонения φ.
      Колебания, которые описывает полученное уравнение, в общем случае не являются простыми гармоническими. Однако, если смещения малы, т.е. угол φ мал, то sinφ ~ φ и тогда уравнение движения принимает вид:
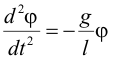или
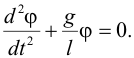Обозначая производную по времени с помощью точек над функцией φ(t), можно также записать
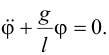Общим решением данного уравнения является функция
где циклическая частота ω и период колебаний Т задаются выражениями
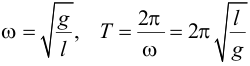а амплитуда А и начальная фаза φ0 задаются начальными условиями, т.е. отклонением груза от положения равновесия и скоростью его движения в момент времени t = 0. Заметим, что ω и Т не зависят от массы груза, а определяются только длиной нити l и ускорением свободного падения g.
 
     Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести (рис. 2). В отличие от математического маятника, который является идеализированным объектом, массу такого тела нельзя считать точечной.
 
Рис. 2. Колебания физического маятника.
 
Движение физического маятника можно описать с помощью его центра масс. Как известно, центр масс системы движется как материальная точка, в которой сосредоточена вся масса системы, и на которую действует сумма всех внешних сил, приложенных к системе. В поле тяжести центр масс совпадает с центром тяжести. На рис. 2 положение центра масс обозначено С, а в точке О находится ось подвеса. Расстояние от т. О до т. С обозначено d.
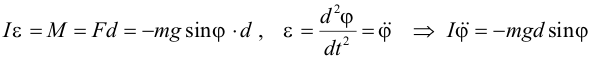     Применяя основной закон динамики вращательного движения , где M – момент внешних сил, I – момент инерции тела, а ε – угловое ускорение, получаем дифференциальное уравнение движения физического маятника:
или
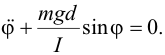Так же, как и в случае математического маятника, будем рассматривать только малые колебания около положения равновесия. В этом случае sinφ ~ φ, откуда получаем
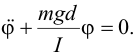Решением этого уравнения является функция
где циклическая частота ω и период колебаний Т задаются выражениями
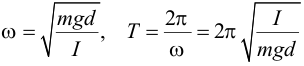Таким образом, малые колебания физического маятника являются гармоническими.
      Длина математического маятника, при которой его период колебаний равен периоду колебаний физического маятника, называется приведенной длиной физического маятника. Приведенную длину lпр легко определить, приравняв соответствующие выражения для периодов колебаний:
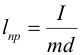Здесь I – момент инерции физического маятника, m – его масса, d − расстояние от точки подвеса до центра масс физического маятника.
 
Описание экспериментальной установки
 
     Лабораторная установка состоит из закрепленного в верхнем конце стержня с массивным шарообразным грузом и секундомера. Через верхний конец стержня проходит ось вращения (рис. 3). Груз можно перемещать по стержню, меняя таким образом распределение масс вдоль физического маятника, что приводит к изменению его момента инерции относительно оси вращения. При проведении опытов, с помощью компьютерной мышки можно контролировать 2 параметра: расстояние от оси вращения до центра масс маятника d (совпадающего с центром масс шара) и начальный угол отклонения от вертикали φ0. Выбранные значения d и φ0 отображаются в окне приложения. Запуск и остановка секундомера осуществляются с помощью кнопки «старт/стоп» на панели прибора, обнулить показания можно с помощью кнопки «сброс».
 
 
Рис. 3. Окно виртуального практикума.
 
Выполнение опыта
 
1. Исследуйте колебания физического маятника при различных начальных углах отклонения φ0 и различных расстояниях до центра масс d. Как меняется период колебаний при уменьшении d?
 
2. Выполните измерения периода колебаний при различных значениях φ0 и фиксированном d. Убедитесь, что при условии малости φ0 период колебаний T физического маятника не зависит от амплитуды (начального угла отклонения), т.е. колебания являются гармоническими: φ(t) = Acos(ωt+φ0). Для этого следует заполнить таблицу: (d = (выбранное значение) , м)
 

 φ0


 Т

50

100

150

200

300

400

500

600

700

800

1100

Т5, с

 

 

 

 

 

 

 

 

 

 

 

Т, с

 

 

 

 

 

 

 

 

 

 

 
 
Внимание! Для повышения точности измерений периода Т, следует измерять длительность не менее 5 полных колебаний, а затем по полученной величине  Т5 вычислить период одного колебания: Т = Т5/5.
 
3. Считая, что лабораторный маятник является математическим, из формулы для периода колебаний математического маятника
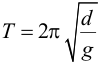выразите ускорение свободного падения g и, пользуясь данными таблицы, рассчитайте величину g исходя из результатов измерений T для трех углов отклонения φ0 = 50, 100, 150.
 
 
Контрольные вопросы
 
  1. По данным построенной вами таблицы нарисуйте примерный график зависимости периода колебаний физического маятника Т от начального угла отклонения φ0 и объясните его вид.
  2. Можно ли при вычислении величины g использовать данные по величине периода колебаний T из измерений для больших углов отклонения φ0?
  3. Как изменяется значение g при изменении широты и долготы местности и высоты над уровнем моря?
  4. При каком значении начального угла отклонения разница в величине T  достигает 0,2 с по сравнению с T при φ0 = 100 ?
  5. Какие виды колебаний вы знаете? Изобразите их схематические графики.
  6. Какие колебания называются гармоническими? Что такое амплитуда, период, частота, фаза колебаний?
  7. Дайте определение физического маятника и математического маятника. Можно ли математический маятник назвать физическим маятником?
  8. Момент какой силы вызывает колебания физического маятника? Запишите выражение для момента этой силы и укажите от чего он зависит.
  9. Запишите уравнение колебаний физического маятника. Какие упрощения были сделаны при его выводе? К какому типу уравнений оно относится и как выглядит его общее решение?
  10. Какую операцию над функцией в физике обозначают с помощью точек над символом?
  11. Что такое момент инерции, какова его роль во вращательном движении?
  12. Как определяется момент инерции одной материальной точки, системы точек, твердого тела? В каких единицах измеряется момент инерции?
  13. Что общего, и каково различие в понятиях «масса» и «момент инерции»?
  14. Как будет меняться момент инерции лабораторного маятника, если груз приближать к оси вращения? Как это повлияет на частоту колебаний?
  15. Что называют приведенной длиной физического маятника?
 
Рекомендуемая литература
 
  1. Савельев И.В. Курс общей физики. Т. 1. – М.: Наука, 1986-1988.
  2. Макаров Е.Ф. Озеров Р.П. Физика для химико-технологических специальностей. – М.: Научный мир, 2002. – 624 с.
  3. Джанколи Д. Физика. В 2-х тт., Т.1. – М.: Мир, 1989.
  4. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1990.
  5. Фриш С.Э., Тиморева А.В. Курс общей физики. Т. 1,2. – М.: Гос. изд. физ.-мат. лит., 1961.