УМК | Об авторах

111

Приложение

1. Операции над векторами

Скалярным произведением векторов

называется произведение их длин на косинус угла между ними:

Свойства скалярного произведения:

Векторным произведением векторов

называется вектор

, который обладает следующими свойствами:

1) Длина вектора

равна:

где φ – угол между векторами

2) Вектор

перпендикулярен плоскости, в которой лежат вектора-сомножители

3) Вектор

направлен так, что поворот от вектора

к вектору

осуществляется против часовой стрелки, если смотреть из конца вектора

(рис. 1). В этом случае говорят, что вектора

образуют правую тройку векторов. В качестве простого примера заметим, что орты правой декартовой системы координат образуют правую тройку:

(рис. 2). Направление вектора

можно определить также с помощью так называемого правила правой руки: если средний палец правой руки направить вдоль вектора

, а указательный вдоль вектора

, то вытянутый большой палец даст направление вектора

в пространстве (рис. 3). Векторное произведение обозначается с помощью квадратных скобок, например

, либо

Рис. 1. Положение вектора

относительно векторов-сомножителей

Рис. 2. Правая декартова система координат,

Рис. 3. Нахождение векторного произведения с помощью правила правой руки.

Если известны декартовы координаты векторов-сомножителей

то результат векторного произведения можно найти с помощью следующего определителя:

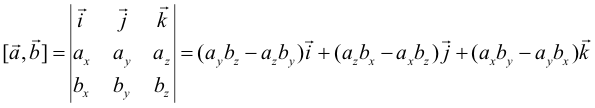В отличие от скалярного произведения, векторное произведение антикоммутативно:

Произведение коллинеарных векторов (т.е. векторов, лежащих на одной прямой или на параллельных прямых) всегда дает нулевой вектор, например

Правила дифференцирования векторов, зависящих от некоторой скалярной переменной t:

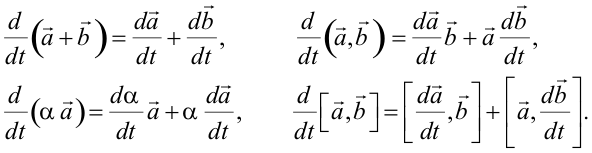2. Таблица производных и интегралов

3. Физические постоянные

4. Единицы измерения физических величин

5. Десятичные приставки к названиям единиц

6. Греческий алфавит