2.1. Электронная оболочка атома

2.2. Периодическая система и электронная структура атомов

2.3. Вопросы и задания

2.1. Электронная оболочка атома

Квантовая механика описывает движение электрона в атоме при помощи волновой функции Ψ. Общий вид этой функции находится из уравнения Шредингера, которое связывает волновую функцию Ψ с потенциальной энергией электрона Е_пот и его полной энергией Е:

,

где первые три члена - это сумма вторых производных волновой функции по координатам х, у и z (часто эту сумму обозначают символом ²Ψ); m - масса электрона; h - постоянная Планка.

Решение уравнения Шредингера связано с большими математическими трудностями. Оно точно решено для атома водорода и для одноэлектронных ионов Не⁺, Li²⁺ и Н₂⁺. Решая уравнение Шредингера, находят значения Ψ-функций, характеризующие вероятность нахождения электрона в некотором пространстве вблизи ядра атома, а также определяют возможные энергетические состояния электрона. Физический смысл Ψ-функции заключается в следующем: вероятность нахождения электрона в некотором объеме пространства пропорциональна квадрату амплитуды волны или же квадрату функции Ψ². Различным функциям Ψ Ψ₁, Ψ₂, Ψ₃,…Ψ_n соответствуют свои квантованные значения энергии Е₁, Е₂, Е₃,...Е_n. Сама волновая функция Ψ - это мера амплитуды электронной волны в некотором малом объеме пространства с координатами х, у, и z, а квадрат волновой функции Ψ² выражает вероятность местонахождения электрона в определенном месте пространства с координатами х, у, и z. Вероятность местонахождения электрона зависит от его энергетического состояния. Электрон может находиться в любом месте пространства, но в области, где значения Ψ² выше, он пребывает чаще, и эти области соответствуют минимальной энергии электрона.

Совокупность мест пространства, где квадрат функции Ψ² имеет максимальное значение, называется электронной орбиталью или электронным облаком атома. Плотность участков электронного облака пропорциональна вероятности нахождения в них электрона. Величина Ψ² выражает вероятность на единицу объема. Чтобы найти вероятность нахождения электрона в сферическом слое радиусом r и бесконечно малой толщиной dr, следует умножить Ψ² на 4πr²dr. Вероятность нахождения электрона в сферическом слое радиуса r толщиной dr называют плотностью электронного облака:

D = 4πr²Ψ ².

На рис. 2.1, а показана точками форма электронной орбитали атома водорода с n = 1. Окружность - это условное место максимальной вероятности местонахождения электрона, например 90 или 95 % электронного облака сосредоточено в области, непосредственно прилегающей к этой окружности. Рисунок сделан на плоскости. В пространстве это будет шаровая поверхность, охватывающая ту же часть электронного облака.

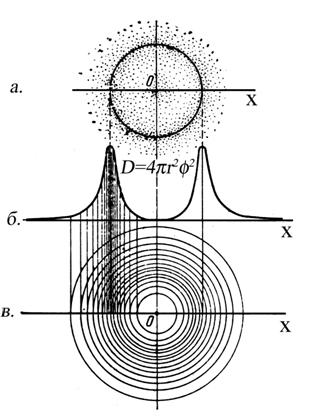
Рис. 2.1. Вероятность нахождения электрона в пространстве около ядра

На рис. 2.1, б представлен разрез вдоль оси ОХ пространства вероятности нахождения электрона. Интересно отметить, что максимум вероятности нахождения электрона, т. е. радиус орбитали, точно совпадает с радиусом орбиты, вычисленной в предположении вращения электрона вокруг ядра, r = 0,53 · 10^-10 м. Этим подтверждается волновое и корпускулярное поведение электрона. На рис. 2.1, в изображен разрез электронного облака плоскостью, а концентрические окружности - это линии одинаковой электронной плотности. Как и на предыдущих рисунках, окружность с r = 0,53 ´10^-10 м отвечает максимальной электронной плотности. Такого типа диаграммы называются контурными диаграммами электронной плотности и широко используются для представления о смещении электронных плотностей атомов относительно ядра при образовании химической связи. Изображение электронного облака в виде зависимости его плотности D от радиуса очень наглядно, однако часто пользуются просто квадратом волновой функции Ψ² и строят диаграммы, откладывая Ψ² в зависимости от расстояния. Исходя из формулы

,

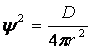очевидно, при r = 0, т. е. в области ядра, Ψ ² будет бесконечно большой величиной и по мере увеличения радиуса Ψ ² уменьшается, стремясь к нулю при r → ∞ (рис. 2.2).

Решение уравнения Шредингера даже для атома водорода - очень сложная задача, так как это уравнение имеет бесконечно большое число решений в связи с тем, что энергия электрона может принимать бесконечно большое число квантованных значений. Однако все решения можно разделить на три серии и ограничиться только теми значениями энергии, которые один электрон может принимать в поле ядра атома водорода (протона). Три серии решений уравнения объединяются значениями связанных между собой квантовых чисел

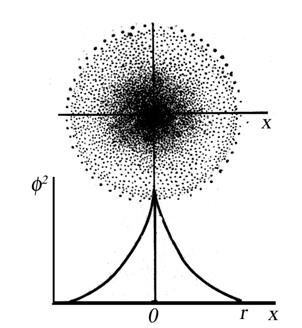
Рис. 2.2. Зависимость квадрата волновой функции от расстояния

Главное квантовое число n. Оно может принимать значения от 1 до бесконечности, которые определяют:

¨            номер энергетического уровня (в теории Бора – номер орбиты);

¨            интервал энергий электронов, находящихся на этом уровне;

¨            размеры орбиталей (в теории Бора – радиусы орбит);

¨            число подуровней данного энергетического уровня;

¨            в Периодической системе Д. И. Менделеева значению главного квантового числа соответствует номер периода.

Иногда пользуются буквенными обозначениями главного квантового числа, т. е. каждому численному значению n соответствует определенное буквенное обозначение:

Таблица 2.1

Буквенные обозначения главного квантового числа

Орбитальное квантовое число ℓ. Орбитальное квантовое число определяет момент импульса электрона, точное значение его энергии и форму орбиталей. Орбитальное квантовое число зависит от главного квантового числа и принимает следующие значения: ℓ = 0, 1, … ,(n – 1), причем каждому значению главного квантового числа n соответствует n значений орбитального квантового числа ℓ. Например, если n = 1, то ℓ принимает только одно значение (ℓ = 0), при n = 2 величина ℓ принимает два значения: 0 и 1 и т. д. Каждому численному значению ℓ соответствует определенная геометрическая форма орбиталей и приписывается буквенное обозначение.

Таблица 2.2

Число подуровней, определяемое значением n

Любой подуровень определяется двумя квантовыми числами - главным (при записи обычно указывают численное значение) и орбитальным (при записи обычно используют буквенное обозначение). Например, энергетический подуровень, для которого n = 2 и ℓ = 1, следует записать так: 2p-подуровень. Все орбитали с одинаковыми значениями ℓ имеют одинаковую геометрическую форму и, в зависимости от значений главного квантового числа, различаются размерами. Так, все орбитали, для которых ℓ = 0 (s-орбитали), имеют форму сферы, но различаются радиусами, в зависимости от значения главного квантового числа n. Чем больше значение n, тем больше размеры орбиталей, например, 1s-орбиталь имеет наименьшие размеры, радиус 2s-орбитали больше, 3s- еще больше.

Магнитное квантовое число m. Вращение электрона вокруг ядра можно сравнить с движением тока по замкнутому контуру. При этом возникает магнитное поле, напряженность которого направлена перпендикулярно плоскости вращения электрона. Если атом находится во внешнем магнитном поле, то, согласно квантовомеханическим представлениям, его электроны должны расположиться так, чтобы проекции их магнитных моментов на направление этого поля были целочисленными. При этом они могут принимать как отрицательные, так и положительные значения, включая нулевое. Численное значение проекции магнитного момента и является магнитным квантовым числом. Если значение орбитального квантового числа равно ℓ, то магнитное квантовое число будет принимать значения от –ℓ до +ℓ, включая ноль. Общее количество значений будет равно 2ℓ + 1.

Таблица 2.3

Число орбиталей на подуровне

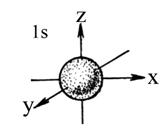
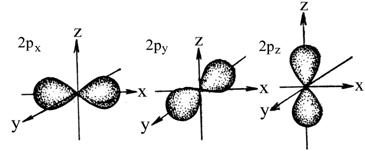
 Физический смысл магнитного квантового числа заключается в следующем. В спектрах атомов, помещенных во внешнее магнитное поле, обнаруживается дополнительное расщепление спектральных линий. Возникновение новых близколежащих линий свидетельствует о том, что в магнитном поле энергия электронов изменяется. Но это возможно только в случае различной взаимной ориентации электронных облаков. Обнаружилось, что все s-подуровни в несильном постоянном магнитном поле не расщепляются. Это говорит о том, что s-электронное облако имеет шаровую симметрию (рис. 2.3, а). р-подуровни расщепляются в магнитном поле на три близкие линии. Это указывает на три различных типа ориентации р-облаков в пространстве. Расчеты показывают, что область максимального значения квадрата волновой функции р-орбиталей имеет форму, напоминающую гантель (рис. 2.3, б). Так как возможны три различных направления р-орбиталей в пространстве, то удобно их расположить вдоль координатных oceй и обозначить р_x, р_у и р_z.

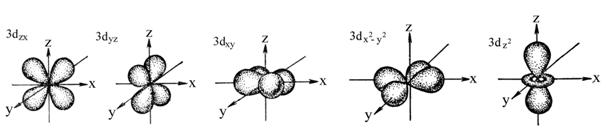
d-подуровень дает в магнитном поле пять близколежащих линий, что указывает на пять различных способов их ориентации в пространстве (рис. 2.1, в). Форма d-облаков значительно сложнее формы р-облаков. Четыре d-облака схожи по внешнему виду между собой, каждое из них как бы составлено из двух расположенных под прямым углом гантелей.

а

б

в

Рис. 2.3. Формы и пространственная ориентация электронных облаков 1s-, 2p- и 3d-электронов

Принято три такие d-орбитали располагать в трех плоскостях хz, уz и ху между координатными осями. Их обозначают соответственно d_xz, d_yz, d_xy. Четвертую d-орбиталь, так же как и орбиталь d_xy, располагают в плоскости ху, но направляют вдоль координатных осей х и у. Эту орбиталь обозначают d_x²_-у². Форма пятой орбитали отличается от остальных: она напоминает гантель, но между шарами в плоскости ху лежит кольцевая область повышенной электронной плоскости. Эту d-орбиталь принято располагать перпендикулярно плоскости d _x²_-у² и d_xy орбиталей, т. е. направляя ее вдоль оси z (как и орбиталь р_z). Ее обозначают d_z². Несмотря на различную форму d-орбиталей квадрат волновой функции Ψ² и плотность D = 4πr² Ψ ² для каждой орбитали одинаковы, что говорит о равновероятности нахождения электрона на любой из этих орбиталей, и их энергетической равноценности.

Если одному и тому же энергетически равноценному состоянию отвечает несколько орбиталей различной ориентации или формы, то такие орбитали называют вырожденными, а само явление энергетической равноценности различных орбиталей называют вырождением. S-состоянию отвечает только одна орбиталь, и явление вырождения к ней неприменимо; р-состоянию отвечают три орбитали, и говорят, что р-состояние вырождено трехкратно. Аналогично, d-состояние вырождено пятикратно, а f-состояние - семикратно.

Когда на одном уровне имеется несколько подуровней s, p, d и f, то энергия их возрастает в направлении от s к f.

Принято каждую орбиталь символически изображать квадратом. S-подуровень состоит из одного квадрата, р-подуровень - из трех квадратов, d-подуровень - из пяти и, наконец, f-подуровень - из семи квадратов:

Подуровни обозначают буквами s, p, d или f, а цифрой перед буквой указывают номер уровня или главное квантовое число. Например, запись Зр означает, что речь идет о р-подуровне третьего уровня, т. е. n = 3, ℓ = 1. 4f означает f-подуровень четвертого, энергетического уровня: n = 4, ℓ = 3.

Спиновое квантовое число (спин электрона), S. Для полной характеристики поведения электрона в атоме оказалось недостаточно трех рассмотренных выше квантовых чисел. Тщательное изучение тонкой структуры спектральных линий показало, что два электрона, имеющие одни и те же значения n, ℓ и m, т. е. одни и те же энергетические характеристики, ту же форму орбитали и одинаковую ориентацию, могут различаться некоторым особым магнитным свойством, которое не поддается объяснению с точки зрения классической механики и обусловливает магнитный момент электрона. Эти два электрона вращаются в различных направлениях (например, по часовой стрелке и против). Это вращение сообщает электрону магнитный и механический моменты, что характеризуется величиной, получившей название «спин». Спин электрона может принимать два противоположных значения, поэтому вводится спиновое квантовое число. Спиновое квантовое число принимает только два значения: S = + и S = -.

Электроны с положительным или отрицательным спинами обозначаются стрелками, направленными соответственно вверх или вниз и помещаемыми в квадрат, изображающий орбиталь. Так, символ Н₁ обозначает основное состояние электрона атома водорода, находящегося на первом энергетическом уровне n = 1 в s-состоянии (ℓ= 0) и имеющего спин S = +.

Для атома водорода, т. е. для системы «один протон и один электрон», спин электрона не влияет на энергетические или другие характеристики атома, но без представления о спине не удается объяснить возникновение молекулы Н₂ из двух нейтральных атомов водорода. Благодаря введению спинового квантового числа, подсчитывается число электронов на любом уровне и подуровне и объясняются магнитные свойства атомов, ионов и молекул. У атомов, имеющих больше одного электрона в соответствии с многочисленными теоретическими предпосылками, подтвержденными экспериментальными данными, не может быть двух электронов или более с одинаковыми значениями всех четырех квантовых чисел. Это принцип (или запрет) Паули. Любые два электрона в атоме должны отличаться, по крайней мере, значением одного из квантовых чисел. Двум электронам атома «запрещено» быть во всех отношениях похожими друг на друга.

Атом водорода в основном состоянии характеризуется следующим набором квантовых чисел: n = 1, ℓ = 0, m = 0, S = +. В этой электронной орбитали нельзя разместить еще один электрон с тем же набором квантовых чисел, т. е. состояние  не допустимо, но можно поместить ещё один электрон, отличающийся значением спинового квантового числа: n = 1, ℓ = 0, m = 0, S = -, что изобразится так: .

Принцип Паули запрещает нахождение на той же орбитали третьего электрона, так как это означало бы, что у двух из них все четыре квантовых числа одинаковы. На одной орбитали или в одной ячейке могут находиться только два электрона, причем только с противоположными спинами. Два электрона, находящиеся на одной орбитали, т. е. имеющие одинаковые значения квантовых чисел n, ℓ и m, но различные значения спинового квантового числа, называются спаренными. Электроны, размещенные по одному на орбиталях одного и того же подуровня, называются неспаренными. Например, в состоянии (I) имеется три неспаренных электрона, в состоянии (II) имеется два спаренных электрона и два неспаренных, а в состоянии (III) все электроны спарены:

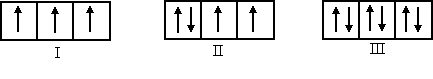
Наличие спаренных или неспаренных электронов в атомах, ионах или молекулах устанавливается экспериментально изучением магнитных свойств. Вещества c неспаренными электронами парамагнитны, т. е. эти вещества проводят магнитные силовые линии лучше, чем вакуум, и магнитное поле втягивает эти вещества. Это вызвано взаимодействием спинов электронов как элементарных магнитов с внешним магнитным полем. Парамагнитны атомы водорода.

Вещества, имеющие спаренные электроны, диамагнитны, т. е. они проводят магнитные силовые линии хуже, чем вакуум, и магнитное поле их выталкивает. Диамагнитны молекулы H₂, N₂O₄, атомы Не, Аr и др.

Увеличение числа электронов в атоме подчиняется определенным законам, что приводит к строгому расположению элементов в периодической системе и периодическому повторению их свойств. Рассмотрим некоторые основные положения электронного строения атомов.

В многоэлектронных атомах относительное энергетическое расположение уровней и подуровней, форма электронных орбиталей и их направление в основном повторяют картину одноэлектронного атома водорода. Учитывая это, применяя принцип Паули и пользуясь набором четырех квантовых чисел, нетрудно рассчитать число подуровней на каждом уровне (по числу значений ℓ для данного n), число орбиталей на каждом подуровне (по числу возможных значений m для данного значения ℓ) и, зная, что на каждой орбитали не может быть больше двух электронов (S = +, S= -), число электронов на каждом подуровне (удвоенное число значений m) и каждом уровне (удвоенное число всех орбиталей уровня).

Например, на первом энергетическом уровне могут находиться только два электрона, так как при n = ℓ ℓ может принимать только одно значение ℓ = n – 1 = 0: возможно только s-состояние. При ℓ = 0 m = 0, т. е. имеется одна s-орбиталь, на которой размещаются два электрона с разными спинами: S =+, S =-.

Другой пример. Четвертый уровень, n = 4 и ℓ может принимать четыре значения 0, 1, 2, 3, т. е. четвертый уровень разделяется на четыре подуровня. При ℓ = 0: m = 0 - это s-орбиталь с двумя электронами. При ℓ = 1 m = -1, 0, +1 - это р-подуровень с тремя орбиталями, каждая из которых содержит по два электрона. Всего на р-подуровне 6 электронов. При ℓ = 2: m = -2, -1, 0, +1, +2, т. е. это d-подуровень с пятью орбиталями, содержащий 10 электронов.  Наконец, при ℓ = 3: m = -3, -2, -1, 0, +1, +2, +3, т. е. имеется еще один подуровень f с семью орбиталями, содержащими 14 электронов. Всего на четвертом уровне содержится 2 + 6 + 10 + 14 = 32 электрона. Строение этого уровня можно представить схемой:

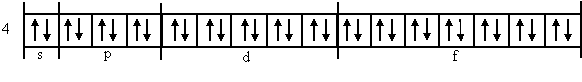
Схема распределения электронов по уровням и подуровням первых четырех энергетических уровней водородоподобного атома:

Мы приходим к двум выводам:

¨            с ростом главного квантового числа емкость энергетических уровней возрастает и для 1, 2, 3 и 4-го уровней составляет 2, 8, 18 и 32 электрона, что совпадает с максимальным числом элементов в 1 - 5-м периодах периодической системы;

¨            в каждом следующем вышестоящем уровне сохраняется электронная структура предыдущего уровня и прибавляется новый подуровень. Например, четвертый уровень имеет структуру третьего уровня (s + p + d-подуровни) и получает дополнительно новый f-подуровень. Он состоит, следовательно, из четырех подуровней: s + p + d + f.

Принцип наименьшей энергии. При заполнении электронами уровней и подуровней последовательность размещения электронов в атоме должна отвечать как наименьшей энергии электрона, так и наименьшей энергии атома в целом. Электрон не занимает вышележащий уровень, если в нижележащем уровне есть места, располагаясь на которых, он будет обладать меньшей энергией. Этот принцип выражает общие термодинамические требования к устойчивости систем: максимуму устойчивости соответствует минимум энергии. В состоянии максимальной устойчивости электронной системы в атоме связь электронов с ядром наиболее прочна.

Правило (n + ℓ), или правило Клечковского. Вследствие взаимодействия электронов между собой в многоэлектронных атомах порядок заполнения уровней и подуровней отличается от ожидаемого в соответствии с расположением энергетических уровней в атоме водорода. Правило суммы (n + ℓ) позволяет предвидеть отличия в расположении энергетических уровней у многоэлектронных атомов от атома водорода.

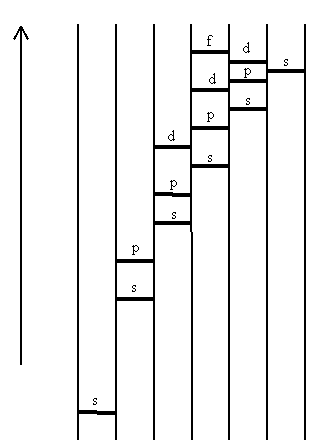
Рис. 2.4. Порядок заполнения электронами энергетических уровней и подуровней

Энергия электрона определяется в основном значениями главного n и побочного ℓ квантовых чисел, и поэтому сначала заполняются те подуровни, для которых сумма значений квантовых чисел n + ℓ является наименьшей. Например, энергия подуровня 4s меньше, чем 3d, так как для 4s-подуровня n + ℓ = 4 + 0 = 4, а для 3d-подуровня n + ℓ = 3 + 2 = 5, поэтому электрон должен сначала вступать на подуровень 4s, а не на 3d (в атоме водорода энергетически более выгоден подуровень 3d).

Если для двух подуровней суммы значений n и ℓ равны, то сначала идет заполнение подуровня с меньшим значением n.

На схеме показано схематически относительное расположение энергетических уровней и подуровней многоэлектронных атомов, найденное при помощи подсчета сумм (n + ℓ) для подуровней различных уровней. Только первые два уровня повторяют структуру атома водорода. После заполнения первых двух уровней и 3s- и 3р-подуровней следующего уровня электрон не вступает, как это ожидалось бы, на 3й-подуровень а, минуя его, идет на 4s-noдуровень.

Таким образом, последовательность энергетических состояний в порядке возрастания энергии орбитали многоэлектронных атомов можно представить следующей схемой:

1s < 2s < 2p < 3s <3 p < 4s ~ 3d < 4p < 5s ~ 4d < 5p < 6s ~ 5d ~ 4f < 6p и т. д.

 Правило Гунда. Порядок заполнения электронами подуровней формулируется правилом Гунда: в подуровнях р-, d- и f-орбитали сперва заполняются одиночными, неспаренными электронами и лишь потом происходит их заполнение вторыми электронами, т. е. спаривание. Иными словами, при заполнении электронами подуровня суммарное спиновое число подуровня должно быть максимальным. Например, состояние (I) имеет суммарное спиновое число ΣS = +  -  +  =+, а состояние (II) того же подуровня с тем же числом электронов имеет ΣS = +  +  + = +. Второму состоянию отвечает большее суммарное спиновое число, и это состояние предпочтительнее первого.

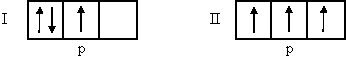
В сложных молекулах и в кристаллах, а также во внешнем магнитном поле правило Гунда часто не соблюдается (теория поля лигандов и теория кристаллического поля).

2.2. Периодическая система и электронная структура атомов

Водород - первый элемент в периодической системе Менделеева. Единственный электрон его атома должен занимать самый низкий энергетический уровень n = 1. Для n = 1 ℓ = 0 и m = 0. Его электронную структуру можно представить формулой H 1s¹, где Н - символ элемента, первая цифра означает номер уровня (n), буква - подуровень, цифра справа вверху показывает число электронов на данном подуровне. На орбитали 1s может быть размещен согласно принципу Паули еще один электрон с противоположным спином. Это имеет место в атоме гелия (№ 2), имеющем структуру Не 1s²:

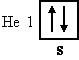
Гелием заканчивается заполнение первого электронного уровня и первый самый короткий период периодической системы. Электрон атома лития (№ 3) вступает во второй уровень n = 2, а сам элемент литий открывает новый - второй период системы. Электронная структура атома лития: Li 1s²2s¹:

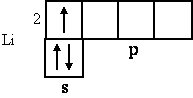
Обращает на себя внимание, что и водород, и литий, имея по одному неспаренному электрону, проявляют во всех своих соединениях одновалентность (например, LiH, LiF, H₂O), а гелий, обладая двумя спаренными электронами, совершенно не склонен к образованию химических соединений, он - нульвалентен. Очень часто, особенно у элементов главных подгрупп, их валентность совпадает с числом неспаренных электронов в атоме.

Следующий электрон - атома бериллия (№ 4) - заканчивает 2s-подуровень. Его структура: Be 1s²2s².

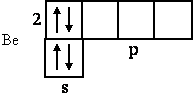
Хотя у бериллия нет неспаренных электронов, он проявляет в своих соединениях валентность, равную двум. Это объясняется тем, что подуровни 2s и 2р энергетически очень близки и незначительной затраты энергии достаточно для перевода одного 2s-электрона на 2р-подуровень; при этом возникает возбужденное состояние с двумя неспаренными электронами:

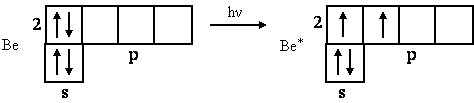
Процесс возбуждения и распаривания электронов можно записать в виде уравнения:

Be 1s²2s²  Be* 1s²2s¹2p¹.

Именно этим и объясняется двухвалентность бериллия.

Бор (№ 5) в невозбужденном состоянии имеет один неспаренный электрон. Известны его неустойчивые и малочисленные соединения типа ВН. В большинстве же соединений бор трехвалентен (В₂О₃, Н₃ВО₃, ВН₃), что объясняется легкостью распаривания 2s-электронов:

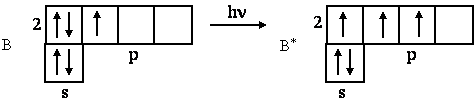
Следующий электрон - у атома углерода (№ 6) - в соответствии с правилом Гунда вступает на р-орбиталь. Углерод, имея два неспаренных электрона, проявляет двухвалентность (например в СО), но чаще - четырехвалентность. В это состояние атом переходит при возбуждении:

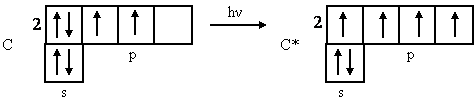
После углерода в ряду элементов азот - кислород - фтор - неон проходит понижение единственно возможного валентного состояния:

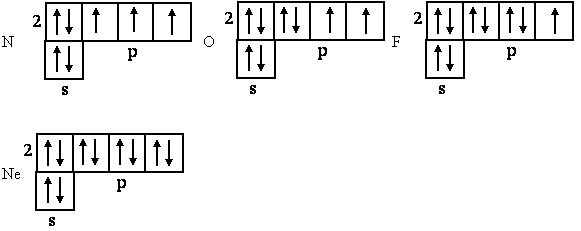
Неон, как и гелий, нульвалентен, так как для распаривания его электронов необходимо их перевести на более высокий третий уровень, что связано с очень большими энергетическими затратами.

Неоном заканчивается заполнение второго энергетического уровня и соответственно второй период таблицы Менделеева. Натрий, имея один электрон на 3s-подуровне, открывает третий период системы Менделеева. Натрий, магний, алюминий и кремний повторяют электронные структуры внешних энергетических уровней лития, бериллия, бора и углерода:

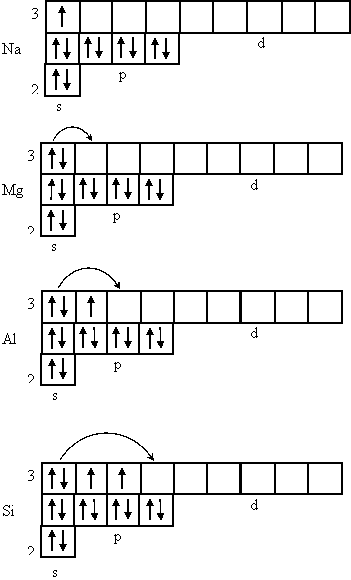
По правилу (n + ℓ) следующий электрон у элемента № 19 калия вступает не на 3d-подуровень, а на 4s, начиная тем самым четвертый период системы Менделеева. Очередной электрон кальция Са ls²2s²2p⁶3s²3p⁶4s² направляется на тот же подуровень 4s

Подуровни 4р и 3d имеют одинаковую сумму n + ℓ: 4 + 1 = 5 и 3 + 2 =5 соответственно. По правилу (n + ℓ) энергетически более выгоден подуровень с меньшим значением главного квантового числа, т. е. подуровень 3d. Поэтому, начиная с № 21 скандия и заканчивая № 30 цинком, десять электронов вступают на второй, считая от внешнего, подуровень 3d.

Заполнение пяти орбиталей 3d-подуровня проходит в соответствии с правилом Гунда: сначала непарными электронами, а затем идет их спаривание:

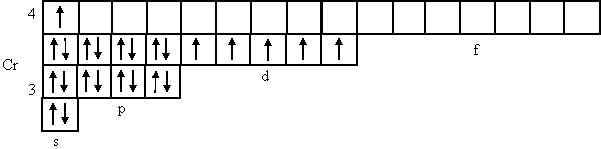
Электронная структура хрома Cr ls²2s²2p⁶3s²3p⁶3d⁵4s¹ интересна тем, что один электрон с 4s-подуровня перешел на 3d-подуровень, после чего подуровень приобрел более устойчивое заполненное наполовину состояние.

У меди, как и у хрома, один электрон с 4s-подуровня переходит на 3d-подуровень, придавая ему устойчивое состояние полного заполнения.

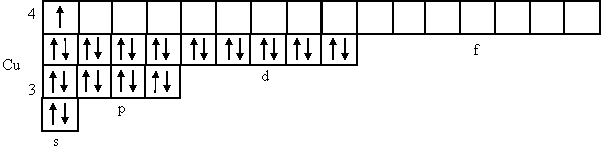
У цинка 4s- и 3d-подуровни полностью заполнены.

Все рассмотренные примеры показывают, что с ростом заряда ядра периодически повторяются сходные электронные структуры и, следовательно, свойства элементов. При рассмотрении электронных структур атомов элементов становится очевидной связь расположения атомов в периодической системе с их строением. Здесь можно отметить следующие закономерности:

¨            Все элементы располагаются в порядке их атомных номеров, т. е. в порядке увеличения числа протонов в ядре.

¨            Химические элементы по структуре невозбужденных атомов располагаются в горизонтальные и вертикальные ряды, носящие название периодов и групп.

¨            Период - это горизонтальный ряд элементов, расположенных в порядке непрерывного роста числа протонов в ядре; в атомах элементов одного периода происходит заполнение электронами близких по энергии подуровней. Номер периода совпадает со значением последнего заполняемого или заполненного s-подуровня. Элементы с особо ярко выраженным сходством следуют один за другим сначала через 8, затем через 18 и через 32 порядковых номера. Поэтому различаются малые и большие периоды. Длина периода определяется числом подуровней, заполняющихся при формировании периода: 1-й период - s-подуровень - 2 элемента; 2-й и 3-й периоды - s- и р-подуровни - 8 элементов; 4-й и 5-й периоды - s-, р- и d-подуровни - 18 элементов; 6-й и 7-й периоды - s-, р-, d- и f-подуровни - 32 элемента.

¨            Группа - вертикальный ряд элементов. В группе объединены элементы, атомы которых различаются числом энергетических уровней, но имеют одинаковую структуру внешних электронных уровней. Элементы одной группы имеют сходные валентные состояния и, следовательно, формулы образуемых соединений. В группе сверху вниз увеличивается число энергетических уровней, и в связи с этим наблюдается закономерное изменение многих свойств атомов, простых веществ и однотипных соединений. Элементы групп разделяются на подгруппы. Элементы, у которых заполняются s- и р-подуровни, образуют главные подгруппы, а элементы, у которых заполняется d-подуровень, - побочные.

¨            Форма периодической системы, по существу, повторяет энергетическую диаграмму заполнения электронами уровней и подуровней многоэлектронного атома.

2.3. Вопросы и задания

2.3.1. Перечислите доводы в пользу того, что одну орбиталь могут занимать только два электрона.

2.3.2. По теории строения атома поглощение света веществом вызывает переход электронов на более высокие энергетические уровни. При возвращении электронов на исходные энергетические уровни энергия выделяется. Если предположить, что энергия поглощенного света равна энергии испускаемого света, то вещество должно быть бесцветным. Почему же вещества бывают цветными?

2.3.3. Может ли частица, состоящая из двух или более атомов, иметь неспаренные s-электроны?

2.3.4. Воспользовавшись правилом Клечковского (правило суммы n + ℓ), предскажите энергетический подуровень, на который поступает электрон, добавляемый к электронным структурам следующих атомов: Са, Zn, Кr, Sr, Cd, Ba, Yb, Hg, Ra. Изобразите схемами исходные и образующиеся электронные структуры.

2.3.5. Сформулируйте правила, которыми определяется порядок заполнения электронами орбиталей атома. Приведите электронные конфигурации невозбужденных атомов K, Mn, Zn, Br.

2.3.6. Напишите электронные формулы атомов элементов пятого периода с порядковыми номерами 37, 43, 48, 52 и 54.

2.3.7. Могут ли электроны иона Rb⁺  находиться на следующих орбиталях: 1) 4s; 2) 3f; 3) 5s; 4) 5p?

2.3.8. Приведите примеры трех частиц (атомы, ионы) с электронной конфигурацией 1s²2s²2p⁶3s²3p⁶.

2.3.9. Напишите электронные формулы атомов элементов четвертого периода: калия, скандия, марганца, цинка, мышьяка и криптона. К какому семейству элементов они относятся?

2.3.10. Какие значения может принимать главное квантовое число n? Объясните смысл значений n = 0 и n = ¥. При каких значениях n электрон обладает наибольшей и при каких - наименьшей энергией? При каких значениях n энергия связи электрона с ядром наибольшая и при каких - наименьшая? Изобразите электронные облака атомов следующих элементов: а) азота; б) кислорода; в) хрома; г) марганца.

2.3.11. В какой последовательности заполняются подуровни, для которых сумма (n + ℓ) последовательно равна 6, 7 и 8? Сколько свободных d-орбиталей имеется в атомах титана и ванадия? Напишите для них электронно-графическую структуру d-подуровня.

2.3.12. Представьте себе, что принцип Паули не соблюдается. Изменится ли от этого структура Периодической системы элементов?

2.3.13. В какой последовательности заполняются подуровни, для которых сумма (n + ℓ) равна последовательно 1, 2 и 3? Напишите электронные формулы атомов элементов шестого периода: цезия, эрбия, гафния, рения, таллия и астата.

2.3.14. В настоящее время предпринимаются попытки синтезировать новые элементы с очень большими порядковыми номерами. Какой из существующих элементов должен быть более всего сходен с элементом № 111? С элементом № 112? С элементом № 118?

2.3.15. Предскажите эмпирические формулы хлоридов элементов с порядковыми номерами 111, 112 и 118.