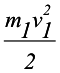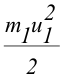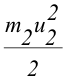На главную
111       111
Лабораторная работа № 3
Изучение законов сохранения
(исследование упругих и неупругих столкновений)
 
Цель работы: проверить экспериментально справедливость законов сохранения импульса и энергии в задачах о неупругих и упругих столкновениях тел.
 
Оборудование, средства измерения: установка с набором шаров на подвесах, весы, разновесы.
 
  
Краткая теория
      
     Когда говорят о столкновении, то подразумевают такое взаимодействие между телами, которое происходит в течение относительно малого промежутка времени в относительно малой области пространства. Другое название таких взаимодействий – удар (столкновение).
     В процессе удара происходит весьма быстрое перераспределение энергии между соударяющимися телами, так что каждое из них после удара будет обладать иной величиной энергии, чем до удара. Дело в том, что при ударе оба тела деформируются, и в результате возникают силы взаимодействия, препятствующие деформациям, т.е. направленные противоположно относительным скоростям соударяющихся тел.
      В физике различают два предельных типа удара: абсолютно упругий удар (АУУ); абсолютно неупругий удар (АНУ). Абсолютно упругим ударом называется такой удар, при котором механическая энергия тел не переходит в другие немеханические виды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию, и тела разлетаются со скоростями, величина и направление которых определяются двумя условиями – сохранением полной механической энергии и сохранением полного импульса системы.
      Абсолютно неупругий удар характеризуется тем, что потенциальной энергии деформации не возникает; кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся.
      Реально в природе абсолютно упругих и абсолютно неупругих тел не существует. Тем не менее, количественные результаты теоретического исследования явления удара в обеих предельных схемах во многих случаях отображают действительные процессы удара с достаточной точностью. Столкновения, происходящие на атомном уровне, т.е. столкновения между атомами, ядрами и элементарными частицами, во многих случаях можно считать  упругими. Однако в макроскопическом мире, с которым мы имеем дело повседневно, абсолютно упругое столкновение – это практически недостижимый идеальный случай, который никогда полностью не реализуется, поскольку в процессе столкновения по крайне мере небольшая часть энергии всегда переходит в тепловую энергию (возможно также в энергию звука или другие аналогичные формы энергии). Тем не менее, при столкновении двух упругих твердых (т.е. обладающих очень малой деформацией) шаров, изготовленных из слоновой кости, закаленной стали, некоторых пластмасс и т.д., упругие свойства выражены настолько сильно, что играют решающую роль в ходе столкновения.
      К неупругим телам можно отнести, например, шары, изготовленные из мягкой глины, пластилина, свинца и других пластических материалов.
 
      Рассмотрим законы сохранения импульса и механической энергии:
1.  Импульс замкнутой системы есть величина постоянная
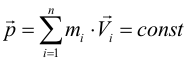2.  Если в замкнутой системе диссипативные силы отсутствуют, то ее полная механическая энергия сохраняется
Под диссипативными силами понимаются силы трения и сопротивления.
 
       Рассмотрим упругое соударение двух тел с массами m1 и m2, скорость первого тела до удара v1, второе тело покоится; скорости тел после удара, соответственно, u1 и u1. Тогда закон сохранения энергии имеет вид
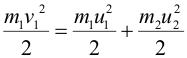Закон сохранения импульса выражается векторным равенством (рис.1):
 
Рис. 1. Закон сохранения импульса.
 
 
      Рассмотрим применение законов сохранения импульса и энергии к центральному абсолютно упругому столкновению двух шаров. Центральным называют удар, при котором все движения происходят вдоль одной линии, проходящей через центр масс (рис. 2).
 
Рис. 2. Упругое столкновение двух частиц.
 
В проекции на ось Х закон сохранения импульса:
Поскольку столкновение предполагается упругим, кинетическая энергия также сохраняется:
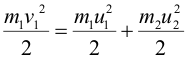 Решая совместно два данных уравнения, получим выражения для скоростей шаров после удара:
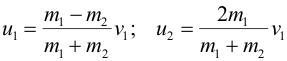Налетающий шар будет продолжать движение в том же направлении или же изменит свое направление на противоположное в зависимости от того, больше ли его масса m1 массы первоначально покоящегося шара m2 или меньше. Если массы m1 и m2 одинаковы, то u1 = 0, u2 = v1. Для m2>>m1 имеем u1 = -v1 и u2 = 0.
 
      Для неупругого центрального соударения двух шаров уравнение закона сохранения импульса:
откуда
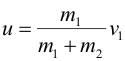Кинетическая энергия системы при неупругом ударе уменьшается. Действительно до удара имеем:
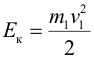после удара
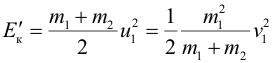Убыль кинетической энергии
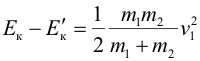ведет к увеличению внутренней энергии системы
 
Описание экспериментальной установки
 
      Установка представляет собой два маятника равной длины с одинаковыми или разными шарами из набора. Правый шар, удерживаемый электромагнитом, бьёт при выключении электромагнита по покоящемуся шару (рис. 3).
Рис. 3. К выводу рабочей формулы.
 
Мерой скорости шара служит величина отброса, отсчитываемого по круговой шкале. Такой метод измерения скорости называется баллистическим. Нетрудно сообразить, что скорость при этом может быть рассчитана по формуле:
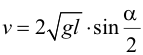где: g – ускорение свободного падения, l – длина подвеса, α – угол отброса по шкале. Данная формула является рабочей формулой для расчета скоростей движущихся шаров в настоящей работе. Длина подвеса лабораторной установки составляет: l=(1,1±0,005) м.
 
Выполнение опыта
 
1. Подберите шары для проведения измерений при упругом ударе. Определите их массы.
2. Включите прибор, нажав кнопку «Вкл./Выкл.».
3. Правый стальной шар m1 отодвинуть в сторону электромагнита и блокировать его в этом положении. Записать значение угла α0.
4. Нажать кнопку «сеть». После столкновения шаров, наблюдать на какие углы α1 и α2 они отклонятся.
5. Измерения провести не менее 10 раз, и определить средние значения углов α1 и α2.
6. Заменить шар m2 на пластилиновый. Повторить измерения согласно пунктов  2–5.
7. Найти скорости шаров до и после столкновения по формуле .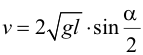
8. Сравнить импульсы системы до столкновения и после него.
9. Рассчитать коэффициент восстановления энергии системы по формуле
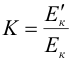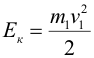где – кинетическая энергия системы до удара, – кинетическая энергия системы после удара. Так как до столкновения во всех опытах движется только один шар m1, то величина определяется кинетической энергией бьющего шара:
После столкновения движутся оба шара, поэтому энергия системы после удара имеет два слагаемых:
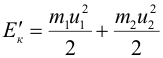10. Представить результаты измерений в виде таблицы, сделать выводы.
 
Таблица результатов измерений и расчетов.
 

№
п/п

a0

a1

a2

v1

u1

u2

m1v1

m1u1

m2u2

K

Упругий удар

1

 

 

 

 

 

 

 

 

 

 

 

 

 

Неупругий удар

2

 

 

 

 

 

 

 

 

 

 

 

 

 
 
В табл. 1 введены следующие обозначения для скоростей: v1 – скорость бьющего шара перед столкновением, u1 – скорость бьющего шара после столкновения, u2 – скорость второго шара (покоившегося до удара) после столкновения.
 
 
Контрольные вопросы
 
  1. Что называется механической системой? Какая система является замкнутой?
  2. Какие взаимодействия считают столкновением?
  3. Какие характеристики ударов вы знаете?
  4. Почему коэффициент восстановления кинетической энергии в опытах К<1?
  5. В чем заключается закон сохранения импульса? В каких системах он выполняется? Почему он является фундаментальным законом природы?
  6. Каким свойством пространства обуславливается справедливость закона сохранения импульса?
  7. Что называется центром масс системы материальных точек? Как движется центр масс замкнутой системы?
  8. В чем различие между понятиями энергии и работы?
  9. Дайте определения и выведите формулы для известных вам видов механической энергии.
  10. Дайте определение потенциальной энергии системы.
  11. Сформулируйте теорему о связи работы и энергии.
  12. Покажите, что силы тяготения, (тяжести, упругости)  консервативны.
  13. В чем заключается закон сохранения механической энергии? Для каких систем он выполняет­ся?
  14. Необходимо ли условие замкнутости системы для выполнения закона сохранения механической энергии?
  15. В чем физическая сущность закона сохранения и превращения энергии? Почему он является фундаментальным законом природы?
  16. Каким свойством времени обусловливается справедливость закона сохранения механической энергии?
  17. Что такое потенциальная яма? потенциальный барьер?
  18. Какие заключения о характере движения тел можно сделать из анализа потенциальных кри­вых?
  19. Как охарактеризовать положения устойчивого и неустойчивого равновесия? В чем их разли­чие?
  20. Чем отличается абсолютно упругий удар от абсолютно неупругого?
  21. Как определить скорости тел после центрального абсолютно упругого удара? Следствием каких законов являются эти выражения?
 
Рекомендуемая литература
 
  1. Савельев И.В. Курс общей физики. Т. 1. – М.: Наука, 1986-1988.
  2. Макаров Е.Ф. Озеров Р.П. Физика для химико-технологических специальностей. – М.: Научный мир, 2002. – 624 с.
  3. Джанколи Д. Физика. В 2-х тт., Т.1. – М.: Мир, 1989.
  4. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1990.
  5. Фриш С.Э., Тиморева А.В. Курс общей физики. Т. 1,2. – М.: Гос. изд. физ.-мат. лит., 1961.