Вектор-функция скалярного аргумента. Производная

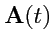
Пусть множество значений вектор-функции скалярного аргумента ${\mathbf A}(t)$ приведено к общему началу в точке 0. Совместим с этой точкой начало декартовой системы координат. Тогда для любого

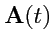
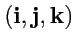
вектор ${\mathbf A}(t)$ может быть разложен по ортам $({\mathbf i},{\mathbf j},{\mathbf k})$ :

Таким образом, задание вектор-функции скалярного аргумента означает задание трех скалярных функций

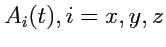
. В этом случае говорят, что вектор-функция задана в декартовой системе координат. (Здесь и далее предполагается, что в сокращенной записи с использованием индексных обозначений ${\mathbf e}_1\equiv{\mathbf i}$ , ${\mathbf e}_2\equiv{\mathbf j}$ , ${\mathbf e}_3\equiv{\mathbf k}$ и соответственно $A_x\equiv A_1$ , $A_y\equiv A_2$ , $A_y\equiv A_3$ , а также используется правило Эйнштейна суммирования по "немым" индексам).

При изменении значения аргумента

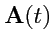
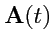
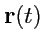
конец вектора ${\mathbf A}(t)$ будет описывать в пространстве кривую, которая называется годографом вектора ${\mathbf A}(t)$ . Например, в механике, годографом радиус-вектора ${\mathbf r}(t)$ будет траектория движения. Согласно (46) уравнения годографа можно получить исключением

изуравнений

что приводит в общем случае к системе уравнений вида:

которая определяет годограф, как линию пересечения двух поверхностей, уравнения которых заданы функциями $\varphi_1$ , $\varphi_2$ .

Пример 2-1. Определить годограф вектор-функции ${\mathbf A}(t)={\mathbf i}\sin(t) + {\mathbf j}\cos(t) - {\mathbf k}\cos(t)$ .

Решение. Исключим параметр

из системы уравнений:

например, как

Первое уравнение определяет круговой цилиндр с образующей, параллельной оси

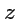
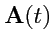
второе - наклонную плоскость. Их пересечением будет эллипс, который и будет в этом случае годографом функции ${\mathbf A}(t)$ (рис. 11).

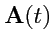
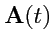
На вектор-функцию можно распространить такие понятия обычного анализа функций, как предел, непрерывность, дифференцируемость. Так, вектор ${\mathbf A}_0$ называется пределом ${\mathbf A}(t)$ при $t\rightarrow t_0$ , если $\lim_{t\to t_0}{\mathbf A}(t)={\mathbf A}_0$ . Функция ${\mathbf A}(t)$ называется непрерывной при

,если

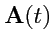
Пусть для ${\mathbf A}(t)$ существует близкое значение ${\mathbf A}(t+\Delta t)$ . Тогда производной вектор-функции поскалярному аргументу называется

Согласно такому определению, производная вектор-функции также является вектор-функцией и поэтому можно аналогично определить и высшие производные.

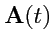
Рассмотрим геометрический смысл производной вектор-функции $\displaystyle{\frac{d{\mathbf A}}{dt}}$ . Если взять два значения ${\mathbf A}(t)$ и ${\mathbf A}(t+\Delta t)$ , то вектор $\Delta{\mathbf A}={\mathbf A}(t+\Delta t)-{\mathbf A}(t)$ будет направлен по секущей

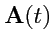
годографа. Тогда, из рис. 12 видно, что при $\Delta t\to 0$ секущая будет стягиваться к касательной и, следовательно, производная вектор-функции направлена по касательной к годографу вектора ${\mathbf A}(t)$ .