Задачи для самостоятельной работы

4. Векторный анализ в криволинейных координатах

4.7. Задачи для самостоятельной работы

I. Доказать, что векторы локального базиса цилиндрической (216) и сферической (220) систем координат являются ортогональными.

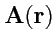
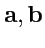
II. Вычислить дивергенции и роторы векторного поля ${\mathbf A}({\mathbf r})$ в сферической и цилиндрической системах координат ( ${\mathbf a},{\mathbf b}$ - постоянные векторы):

$\begin{displaymath} \hspace{-37mm} \begin{array}{lll} \mbox{1.} & ({\mathbf a},{... ...yle{\frac{[{\mathbf a},{\mathbf r}]}{r^3}} \\ [1em] \end{array}\end{displaymath}$

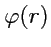
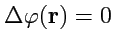
III. Показать прямым вычислением в сферической системе координат, что поле $\varphi(r)$ является гармоническим ( $\Delta\varphi({\mathbf r})=0$ ).

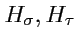
IV. Найти коэффициенты Ламэ $H_\sigma, H_\tau$ для эллиптической системы координат (222).

V. Вычислить градиент скалярной функции

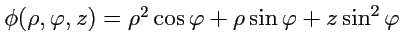
1. $\phi(\rho,\varphi,z)=\rho^2\cos\varphi + \rho\sin\varphi + z\sin^2\varphi$

2. $\phi(r,\theta,\varphi)= r^2\cos\theta + r\sin\theta\cos\varphi$ .

VI. Вычислить ${\rm div}\,{\mathbf A}$ , ${\rm rot}\,{\mathbf A}$ векторного поля ${\mathbf A}({\mathbf r})$

1. ${\mathbf A}(\rho,\varphi,z)=\rho\ {\mathbf e}_\rho + z\sin\varphi\ {\mathbf e}_\varphi + z\tg\varphi\ {\mathbf e}_z$

2. ${\mathbf A}(r,\theta,\varphi) = r\ {\mathbf e}_r + r\cos\theta\tg\varphi\ {\mathbf e}_\theta + r^3\sin\theta\ {\mathbf e}_\varphi$


			Содержание