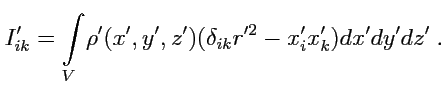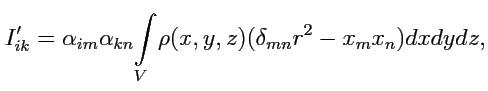5. Основы тензорного анализа
 5.1. Физическое определение тензора
5.1. Физическое определение тензора 
Понятие тензора наиболее естественно возникает при рассмотрении физических задач, связанных с использованием величин, определяющих собственные характеристики исследуемых объектов. Интуитивно
понятно, что эти собственные или
внутренние характеристики должны обладать свойством
инвариантности и не иметь зависимости от способа их применения, который определяется выбором
системы координат. Физические скаляры, такие как масса, заряд и другие, отвечают таким требованиям с очевидностью. Простейшие кинематические величины (скорость, ускорение) имеют векторный характер
и относительно системы координат задаются тройкой чисел, которые при вращении осей изменяются
по правилам (
36) и (
37). Инвариантность в этом случае выражается в том, что,
несмотря на изменение координат, сам вектор, как объект-стрелка, остается совершенно неизменным
и самостоятельным, что позволяет построить "графические" правила (треугольника, параллелограмма
в 1-й гл.) для выполнения алгебраических действий с векторами, а также непротиворечивый символический
способ выполнения дифференциальных операций с векторными полями (Гл.3). Таким образом, использование
векторного способа записи для физических величин и действий над ними, что было сделано Дж. У. Гибсом, позволяет выразить те или иные закономерности в форме, которая полностью соответствует фундаментальному физическому закону - принципу
относительности.
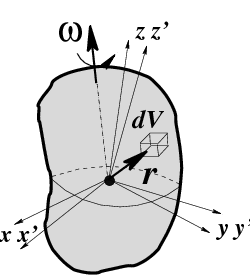
Рис.45 Вращающееся твердое тело
Используя свойство инвариантности, можно построить величины, которые, аналогично скалярам и
векторам можно связать с собственными характеристиками физических объектов. В качестве примера
вычислим кинетическую энергию вращающегося тела произвольной формы (рис.
45). Пусть
тело закреплено в центре инерции и вращается с угловой скоростью
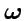
. Тогда, если
вещество распределено по объему с плотностью
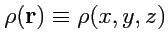
, то
![$\displaystyle E_{kin} = \displaystyle{\frac{1}{2}}\displaystyle{\int\limits_{V}^{}}\rho(x,y,z)[{\boldsymbol \omega},{\mathbf r}]^2 dxdydz.$](img1052.png) |
(243) |
Раскрывая квадрат векторного произведения под знаком интеграла и записывая результат
с использованием индексных обозначений и правила Эйнштейна (Гл.1), получим
что с использованием свойств
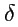
-символа можно переписать как
![$\displaystyle [{\boldsymbol \omega},{\mathbf r}]^2 = \omega_i \omega_k (\delta_{ik}r^2 - x_ix_k)\ ,$](img1054.png) |
(244) |
Тогда, после подстановки (
244) в (
243), выражение для кинетической
энергии принимает вид
![$\displaystyle E_{kin} = \displaystyle{\frac{1}{2}}\left[\displaystyle{\int\limits_{V}^{}}\rho(x,y,z) (\delta_{ik}r^2 - x_ix_k) dxdydz\right] \omega_i \omega_k.$](img1055.png) |
(245) |
Обозначим величину в квадратных скобках как
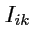
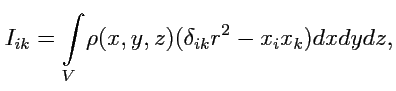 |
(246) |
тогда (
245) можно окончательно представить в форме
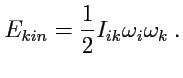 |
(247) |
Так как величина кинетической энергии определяется, помимо кинематических характеристик,
роль которых в данном случе играет угловая скорость, инертными свойствами самого тела, то из
(
247) следует, что свойства "вращательной инерции" связаны с величинами
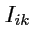
.
Если все значения
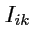
записать в виде матрицы
![$\displaystyle (\hat{{\mathbf I}})_{ik} = \left(\begin{array}{ccc} I_{xx} & I_{x...
...} & I_{yy} & I_{yz} \\ [0.5em] I_{zx} & I_{zy} & I_{zz} \\ \end{array} \right),$](img1059.png) |
(248) |
то (
247) можно записать как двойное скалярное произведение
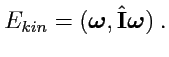 |
(249) |
Чтобы выяснить смысл величин
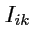
, рассмотрим частный случай, когда
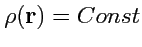
,
а тело имеет форму шара радиуса
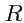
. Тогда матрица
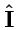
будет иметь вид:
![$\displaystyle (\hat{{\mathbf I}})_{ik} = \displaystyle{\frac{2}{5}}MR^2 \left(\...
... 0 & 0 \\ [0.5em] 0 & 1 & 0 \\ [0.5em] 0 & 0 & 1 \\ \end{array} \right)\ ,\quad$](img1064.png) |
(250) |
где
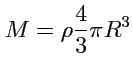
- масса шара. Так как матрица
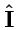
пропорциональна
единичной матрице, то присутствие индексов в обозначении
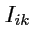
является в этом случае
излишним. Действительно, кинетическая энергия вращения шара, закрепленного в центре, после
подстановки (
250) в (
247) принимает вид
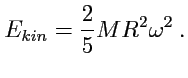 |
(251) |
Величина
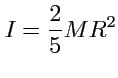
называется моментом инерции шара и является характеристикой
инерции однородного тела сферической формы при вращении. Следует отметить, что в случае шара
выражение для кинетической энергии с очевидностью является инвариантым, поскольку выражается
только через скалярные величины. Для того, чтобы придать какой-либо физический смысл величинам
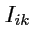
в общем случае, необходимо выяснить какие изменения произойдут с набором этих чисел,
в другой системе координат. Вычислим
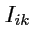
в системе координат
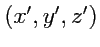
, развернутой
относительно исходной системы
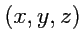
.
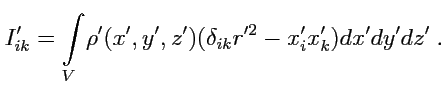 |
(252) |
Новые переменные
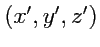
в (
252) связаны c
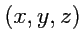
соотношением
(
37)
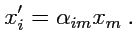 |
(253) |
Так как
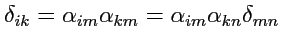
согласно
(
30), а значение якобиана перехода замены переменных (
253)
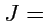
det
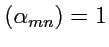
, то
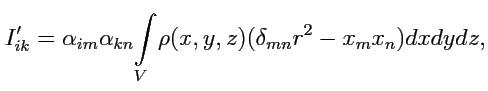 |
(254) |
где также использована замена для формулы
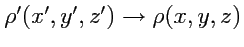
. Как видно,
значение интеграла в точности совпадает с
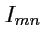
согласно (
246) и это позволяет
выразить
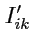
как
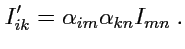 |
(255) |
Закон преобразования для величин
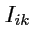
позволяет получить интересное соотношение.
Действительно, вычислим значение величины
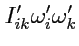
. Тогда
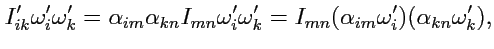 |
(256) |
а так как
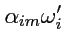
в соответствии с (
30) выражает значения
координат вектора
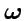
в системе
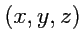
,то
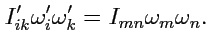 |
(257) |
Полученный результат имеет несколько важных особенностей:
- выражения для значения кинетической энергии в различных системах координат
совершенно одинаковы по форме;
- отмеченная инвариантость обеспечивается билинейным законом преобразования
(255) для
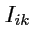 .
.
Эти свойства величин
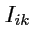
позволяют связать их с собственной характеристикой тела,
которая количественно выражает свойство инерции при вращательном движении. Вся совокупность
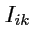
является компонентами (координатами)
одной величины, которая в данном случае
называется
тензором инерции, при этом формула (
248) является одним из
способов записи тензора или его матричным представлением.

![$\displaystyle E_{kin} = \displaystyle{\frac{1}{2}}\displaystyle{\int\limits_{V}^{}}\rho(x,y,z)[{\boldsymbol \omega},{\mathbf r}]^2 dxdydz.$](img1052.png)
![$\displaystyle [{\boldsymbol \omega},{\mathbf r}]^2 = {\boldsymbol \omega}^2 {\m...
... \omega},{\mathbf r})^2 =
\omega_i\omega_i r^2 - \omega_i x_i \omega_k x_k\ ,
$](img1053.png)
![$\displaystyle [{\boldsymbol \omega},{\mathbf r}]^2 = \omega_i \omega_k (\delta_{ik}r^2 - x_ix_k)\ ,$](img1054.png)
![$\displaystyle E_{kin} = \displaystyle{\frac{1}{2}}\left[\displaystyle{\int\limits_{V}^{}}\rho(x,y,z) (\delta_{ik}r^2 - x_ix_k) dxdydz\right] \omega_i \omega_k.$](img1055.png)
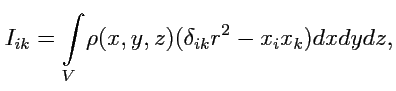
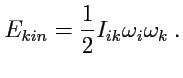
![$\displaystyle (\hat{{\mathbf I}})_{ik} = \left(\begin{array}{ccc} I_{xx} & I_{x...
...} & I_{yy} & I_{yz} \\ [0.5em] I_{zx} & I_{zy} & I_{zz} \\ \end{array} \right),$](img1059.png)
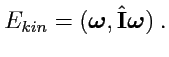
![$\displaystyle (\hat{{\mathbf I}})_{ik} = \displaystyle{\frac{2}{5}}MR^2 \left(\...
... 0 & 0 \\ [0.5em] 0 & 1 & 0 \\ [0.5em] 0 & 0 & 1 \\ \end{array} \right)\ ,\quad$](img1064.png)
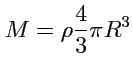 - масса шара. Так как матрица
- масса шара. Так как матрица
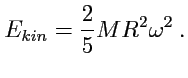
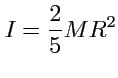 называется моментом инерции шара и является характеристикой
инерции однородного тела сферической формы при вращении. Следует отметить, что в случае шара
выражение для кинетической энергии с очевидностью является инвариантым, поскольку выражается
только через скалярные величины. Для того, чтобы придать какой-либо физический смысл величинам
называется моментом инерции шара и является характеристикой
инерции однородного тела сферической формы при вращении. Следует отметить, что в случае шара
выражение для кинетической энергии с очевидностью является инвариантым, поскольку выражается
только через скалярные величины. Для того, чтобы придать какой-либо физический смысл величинам