5. Основы тензорного анализа
Согласно общему определению, для случая
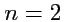
можно получить частное определение:
тензором 2-го ранга называется совокупность 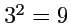 величин
величин 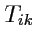 , которые
преобразуются по закону
, которые
преобразуются по закону
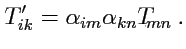 |
(264) |
Рассмотренный выше тензор инерции, согласно закону преобразования (
257) и
определению (
264), является тензором 2-го ранга. Другим примером тензора второго
ранга является
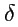
-символ Кронекера. Действительно, компоненты
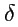
-символа можно
получить как скалярное произведение ортов прямоугольной системы:
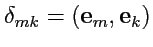 |
(265) |
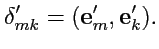 |
(266) |
Используя закон преобразования ортов (
37), а также (
265) и (
266),
получим
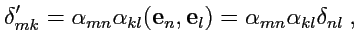 |
(267) |
откуда видно, что
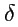
-символ преобразуется как тензор 2-го ранга. Продолжая вычисления
в (
267),
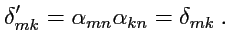 |
(268) |
Таким образом, преобразуясь как тензор 2-го ранга, дельта-символ, в то же время, не меняет
своего вида. Такие тензоры называются инвариантными.
И наконец, тензор 2-го ранга можно получить как прямое произведение двух векторов, тензоров
1-го ранга. Действительно, пусть
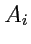
и
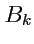
- компоненты векторов
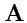
и
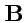
. Тогда,
составляя
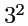
величин
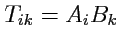
, легко показать, что они преобразуются по закону
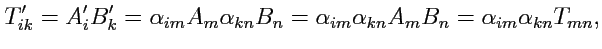 |
(269) |
который соответствует определению тензора 2-го ранга (
264).