5. Основы тензорного анализа
 5.18. Тензорная алгебра в евклидовом пространстве
5.18. Тензорная алгебра в евклидовом пространстве 
Характерной чертой евклидового пространства является возможность расширить число алгебраических
действий с тензорами за счет определения так называемых операций
поднятия и опускания индексов,
что означает изменение характера тензоров. Пусть в евклидовом пространстве задан контравариантный
тензор 1-го ранга
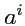
. Рассмотрим набор величин
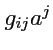
. Согласно правилам тензорной алгебры,
новый набор будет представлять координаты ковариантного тензора первого ранга, для обозначения которого
имеет смысл сохранить тот же символ
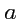
:
Рассмотрим смысл нового ковариантного тензора и то, как он соотносится с вектором

. Учитывая
определение метрического тензора (
342), из (
348) легко получить
т. е.
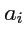
есть скалярное произведение вектора

на базисный вектор
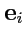
(проекция).
Эти скалярные произведения называются ковариантными координатами вектора

.
Обращение уравнения (
348) определяет операцию поднятия индексов:
Операции поднятия и опускания индексов взаимно обратны, т. е. в результате применения этой
последовательности действий к тензору он не изменяется:
По той же схеме (
348) или (
350) можно поднимать или опускать индексы и у тензоров высших
рангов. В этом случае необходимо ввести общий (ступенчатый) способ записи индексов. Например, если
третий индекс координаты тензора 4-го ранга является контравариантным, а остальные ковариантные, то это можно
явно указать, отмечая пустые места точками
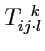
, либо просто оставляя место
для движения индекса:
Важный пример дает выражение (
347), которое показывает, что поднятие (или опускание) индекса
у метрического тензора переводит его в единичный тензор.
В заключение этого раздела отметим, что вводимые новые определения могут быть сформулированы лишь в
евклидовом пространстве и не имеют никакого смысла в аффинном пространстве без метрики, где поднятие
или опускание индексов невозможно. Это же относится и к понятию ковариантных координат вектора.
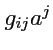 . Согласно правилам тензорной алгебры,
новый набор будет представлять координаты ковариантного тензора первого ранга, для обозначения которого
имеет смысл сохранить тот же символ
. Согласно правилам тензорной алгебры,
новый набор будет представлять координаты ковариантного тензора первого ранга, для обозначения которого
имеет смысл сохранить тот же символ