5. Основы тензорного анализа
 5.17. Евклидово пространство n измерений
5.17. Евклидово пространство n измерений 
До настоящего времени рассматривалась так называемая аффинная геометрия, т. е. некоторое абстрактное

-мерное линейное пространство без метрических свойств, введение которых требует дополнительной
операции, называемой
скалярным произведением векторов и позволяющей определить понятие
евклидова пространства. Зададим на линейном пространстве симметричную билинейную скалярную
функцию
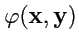
:
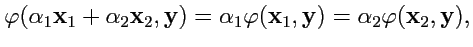 |
(335) |
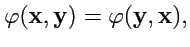 |
(336) |
которая является невырожденной, что эквивалентно условию:
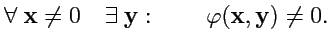 |
(337) |
Тогда эта билинейная функция будет определять скалярное произведение. Так как функция (
335)
задана навсегда, то скалярное произведение можно (и удобно) переобозначить как
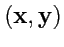
.
Скалярный квадрат вектора
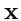
можно вычислить как
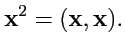 |
(338) |
Два вектора
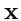
и
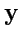
будут называться
ортогональными, если
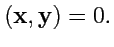 |
(339) |
Длиной вектора называется величина
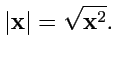 |
(340) |
Евклидово пространство распадается на два больших класса: вещественное
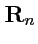
и
комплексное
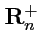
, в зависимости от того, какими являются координаты векторов линейного
пространства. В свою очередь, вещественные евклидовые пространства также делятся на два подкласса:
- собственно евклидово, в котором
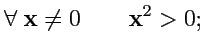 |
(341) |
-
псевдоевклидово, где
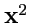
может принимать как положительные, так и отрицательные
значения.
Собственно евклидово пространство является обощением 3-х мерного пространства и с точностью до
изоморфизма для каждого

существует одно собственно евклидово пространство.
Псевдоевклидовы пространства, которые, в частности, используются в специальной теории относительности,
обладают весьма своеобразными свойствами, которые не имеют аналогов в обычной геометрии. Так, из (
341) сразу следует, что длина вектора в этом случае может быть и вещественной, и мнимой,
и даже нулем, хотя сам вектор нулевым может и не быть. Мнимая длина - это единственная комплексная
величина в вещественном псевдоевклидовом пространстве. Для данного

можно построить

различных
псевдоевклидовых пространств.
Как было показано выше, задание билинейной функции
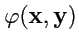
равносильно заданию дважды
ковариантного тензора
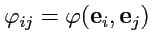
и
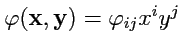
. В случае скалярного произведения
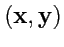
принято называть этот тензор
метрическим (часто просто метрикой) и обозначать его координаты
как
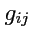
.Тогда
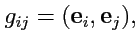 |
(342) |
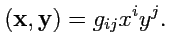 |
(343) |
При
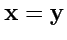
получим скалярный квадрат вектора
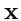
:
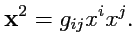 |
(344) |
Условие симметрии скалярного произведения
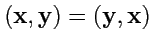
равносильно симметричности
метрического тензора
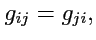 |
(345) |
а условие невырожденности (
337) означает, что
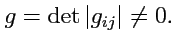 |
(346) |
Свойство (
346) означает, что матрица координат
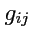
имеет обратную, а ее элементы
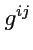
определяют контравариантный метрический тензор
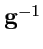
:
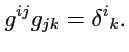 |
(347) |
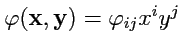 . В случае скалярного произведения
. В случае скалярного произведения