![]() Тема 1. Основания математики
Тема 1. Основания математики
Числа
Интуитивное представление о числе, по–видимому, так же старо, как и само
человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно.
Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно,
владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и
двух людей или двух и многих людей. То, что первобытные люди сначала знали только “один”, “два” и
“много”, подтверждается тем, что в некоторых языках, например в греческом, существуют три
грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее
человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми.
Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел
были прилагательными. Например, слово “три” использовалось только в сочетаниях “три дерева” или
“три человека”; представление о том, что эти множества имеют между собой нечто общее – понятие
троичности – требует высокой степени абстракции. О том, что счет возник раньше появления этого
уровня абстракции, свидетельствует тот факт, что слова “один” и “первый”, равно как “два” и
“второй”, во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами
первобытного счета “один”, “два”, “много”, слова “три” и “третий”, “четыре” и “четвертый” ясно
указывают на взаимосвязь между количественными и порядковыми числительными.
Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно,
позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В
глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке,
выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества
и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких
числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда
распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на
взгляд наборы, состоящие из пяти, шести или семи элементов. А за этой границей установить на глаз
их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном
структурировании элементов. Счет на бирках, по–видимому, был первым приемом, который использовался
в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при
подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень
широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут
свое начало именно от этого способа подсчета.
Важная особенность счета заключается в связи названий чисел с определенной схемой счета.
Например, слово “двадцать три” – не просто термин, означающий вполне определенную (по числу
элементов) группу объектов; это термин составной, означающий “два раза по десять и три”. Здесь
отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие
считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на
ногах. По той же причине использовались основания пять или двадцать. На очень ранних стадиях
развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда
для некоторых измерения или вычислений использовались основания 12 и 60.
Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких
письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа.
Для кочевых племен характерны устные названия чисел, что же касается письменных, то необходимость
в них появилась лишь с переходом к оседлому образу жизни, образованием земледельческих сообществ.
Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для
развития математики.
Древний Египет
Расшифровка системы счисления, созданной в Египте во времена первой династии
(ок. 2850 до н.э.), была существенно облегчена тем, что иероглифические надписи древних египтян
были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние
египтяне использовали только десятичную систему счисления.
Единицу обозначали одной вертикальной
чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число
вертикальных штрихов. (См. сводную таблицу обозначений чисел.) Чтобы записанные таким образом
числа было легко узнавать, вертикальные штрихи иногда объединялись в группы из трех или четырех
черт. Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт
ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку.
Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом,
напоминающим силки; десять силков, т.е. число 1000, египтяне обозначили стилизованным
изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем,
десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного
человека. В итоге древние египтяне могли представлять числа до миллиона. Так, например, с
помощью коллективных символов и повторений уже введенных символов число 6789 в иероглифических
обозначениях можно было бы записать как
Самые древние из дошедших до нас математических записей высечены на камне,
но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на
гораздо более хрупком и недолговечном материале – папирусе. Два таких документа – папирус Ринда,
или египетского писца Ахмеса (ок. 1650 до н.э.) и московский папирус, или папирус Голенищева
(ок. 1850 до н.э.) – служат для нас основными источниками сведений о древнеегипетских арифметике
и геометрии. В этих папирусах более древнее иероглифическое письмо уступило место скорописному
иератическому письму, и это изменение сопровождалось использованием нового принципа обозначения
чисел. Группа одинаковых символов заменялись более простой по начертанию пометой или знаком,
например, девять записывалось как Вавилон
Письменность шумеров является, по-видимому, столь же древней, как и
письменность египтян. Развитие способов представления чисел в Месопотамской долине вначале шло
так же, как и в долине Нила, но затем жители Междуречья ввели совершенно новый принцип.
Вавилоняне делали записи острой палочкой на мягких глиняных табличках, которые затем обжигались
на солнце или в печи. Эти записи оказались исключительно долговечными, а потому, в отличие от
египетских папирусов, дошедших до нас в весьма малом числе экземпляров, в музеях мира хранятся
десятки тысяч клинописных табличек. Однако жесткость материала, на котором жители Месопотамии
делали записи, оказала глубокое влияние на развитие числовых обозначений. Через некоторое время
после того, как Аккад завоевал шумеров, система счисления в Месопотамии стала
шестидесятеричной, хотя сохранилось также и основание 10. Казавшееся правдоподобным
предположение относительно того, почему выбор пал на число 60 как на основу вавилонской системы
счисления, и утверждавшее, будто это связано с тем, что продолжительность земного года считалась
равной 360 дням, не получило подтверждения. Ныне принято считать, что шестидесятеричная система
была выбрана из метрологических соображений: число 60 имеет много делителей.
Для малых чисел вавилонская система счисления в основных чертах напоминала
египетскую. Одна вертикальная клинообразная черта (в раннешумерских табличках – небольшой
полукруг) означала единицу; повторенный нужное число раз, этот знак служил для записи чисел
меньше десяти; для обозначения числа 10 вавилоняне, как и египтяне, ввели новый коллективный
символ – более широкий клиновидный знак с острием, направленным влево, напоминающий по форме
угловую скобку, Повторенный соответствующее число раз, этот знак служил для обозначения
чисел 20, 30, 40 и 50. Принцип повторного использования знаков позволял, например, записать
число 59 в виде Но для записи чисел больше 59 древние вавилоняне впервые использовали новый
принцип – одно из самых выдающихся достижений в развитии систем обозначений чисел – принцип
позиционности, т.е. зависимости значения символа от его местоположения в записи числа.
Вавилоняне заметили, что в качестве коллективных символов более высокого порядка можно применять
уже ранее использованные символы, если они будут занимать в записи числа новое положение левее
предыдущих символов. Так, один клиновидный знак мог
использоваться для обозначения и 1, и 60, и 602, и 603, в
зависимости от занимаемого им в записи числа положения, подобно тому, как
единица в наших обозначениях используется в записях и 10, и 102, и
103, и в числе 1111. При обозначении чисел больше 60 знаки,
выступающие в новом качестве, отличались от старых тем, что символы разбивались
на “места”, или “позиции”, и единицы более высокого порядка располагались
слева. При таком способе записи для обозначения сколь угодно больших чисел уже
не нужно было других символов, кроме уже известных. Например, число 6789 можно
было записать так: Символы для обозначения чисел на вавилонских
глиняных табличках не столь точны, как символы для обозначения чисел на
древнеегипетских папирусах, несмотря на то, что вавилоняне использовали
позиционный принцип. В исключительных случаях вавилоняне применяли сокращенные
формы записи, иногда – с новыми символами для обозначения чисел 100 и 1000, или
использовали принципы умножения или вычитания. Однако превосходство
разработанной в Месопотамии системы счисления отчетливо видно в обозначении
дробей. Здесь не требовалось вводить новые символы. Как и в нашей собственной
десятичной позиционной системе, в древневавилонской системе подразумевалось,
что на первом месте справа от единиц стоят величины, кратные 1/60, на втором
месте – величины кратные 1/602 и т.д. Привычное нам деление часа и
углового или дугового градуса на 60 минут, а одной минуты – на 60 секунд берет
начало от вавилонской системы счисления.
Древняя Греция
В Древней Греции имели хождение две основных системы счисления –
аттическая (или
геродианова) и ионическая (она же александрийская или алфавитная).
Аттическая система счисления использовалась греками, по-видимому, уже к 5 в.
до н.э. По существу это была десятичная система (хотя в ней также было выделено и число
пять), а аттические обозначения чисел использовали повторы коллективных
символов. Черта, обозначавшая единицу, повторенная нужное число раз, означала
числа до четырех. После четырех черт греки вместо пяти черт ввели новый символ
Г, первую букву слова “пента” (пять) (буква Г употреблялась для обозначения
звука “п”, а не “г”). Дойдя до десяти, они ввели еще один новый символ D,
первую букву слова “дека” (десять). Так как система была десятичной, грекам
потребовались новые символы для каждой новой степени числа 10: символ H означал
100 (гекатон), X – 1000 (хилиои), символ M – 10000 (мириои или мириада).
Используя число 5 как промежуточное под-основание системы счисления, греки на
основе принципа умножения комбинировали пятерку с символами степеней числа 10.
Так, число 50 они обозначали символом Вторая принятая в Древней Греции ионическая система счисления –
алфавитная – получила широкое распространение в начале Александрийской эпохи, хотя
возникнуть она могла несколькими столетиями раньше, по всей видимости, уже у пифагорейцев.
Эта более тонкая система счисления была чисто десятичной, и числа в ней обозначались
примерно так же, как в древнеегипетской иератической системе. Используя двадцать четыре буквы
греческого алфавита и, кроме того, еще три архаических знака, ионическая система сопоставила
девять букв первым девяти числам; другие девять букв – первым девяти целым кратным числа десять;
и последние девять символов – первым девяти целым кратным числа 100. Для обозначения первых девяти
целых кратных числа 1000 греки частично воспользовались древневавилонским принципом позиционности,
снова использовав первые девять букв греческого алфавита, снабдив их штрихами слева. Например,
число 6789 в ионической системе записывалось как FYPQ. Чтобы отличить числа от слов, греки над
соответствующей буквой ставили горизонтальную черту. Первоначально числа обозначались прописными
буквами, но позднее сменились на строчные.
Ионическая система первоначально не сильно потеснила уже установившуюся
аттическую или акрофоническую (по начальным буквам слов, означавших числительные) системы
исчисления. По-видимому, официально она была принята в Александрии во времена правления Птолемея
Филадельфийского и в последующие годы распространилась оттуда по всему греческому миру, включая
Аттику. Переход к ионической системе счисления произошел в золотой век древнегреческой математики
и, в частности, при жизни двух величайших математиков античности. Есть нечто большее, чем просто
совпадение, в том, что именно тогда Архимед и Аполлоний работали над
усовершенствованием системы обозначения больших чисел. Архимед, придумавший схему октад
(эквивалентную современному использованию показателей степени числа 10), гордо заявлял в своем
сочинении “Псаммит” (“Исчисление песчинок”), что может численно выразить количество песчинок,
необходимых для того, чтобы заполнить всю известную тогда Вселенную. Изобретенная им система
обозначения чисел включала число, которое ныне можно было бы записать в виде единицы, за которой
следовало бы восемьдесят тысяч миллионов миллионов цифр.
С помощью простого введения диакритических знаков наподобие тех, которые греки
применяли для обозначения тысяч, алфавитное обозначение целых чисел можно было бы легко
приспособить для обозначения десятичных дробей, но этой возможностью они не воспользовались.
Вместо этого для обозначения дробей греки использовали приемы древних египтян и вавилонян.
Египетское влияние в Греции было достаточно сильным, чтобы навязать грекам употребление лишь
аликвотных дробей, однако большие вычислительные удобства системы счисления вавилонян побудили
живших позднее александрийских астрономов перейти к использованию шестидесятеричных дробей.
Переняв систему счисления Древнего Вавилона, греки заменили месопотамскую клинопись своими
буквенными обозначениями. Например, Птолемей записал длину хорды, стягивающей дугу в 120°
окружности радиусом в 60 единиц, как RGNE¢KG¢, т.е. 103 + 55/60 +
23/602 единиц. В более поздний период в вавилонской
шестидесятеричной системе имелся специальный символ для обозначения “пустой”
позиции, и греческие астрономы ввели для этой цели букву омикрон. Неясно, был
ли такой выбор подсказан тем, что с этой буквы начиналось слово оуден (ничто).
Сходство греческой буквы О с современным обозначением нуля может быть чем-то
большим, чем случайное совпадение, но у нас нет точных данных, позволяющих
утверждать это со всей определенностью.
Поскольку греки работали с обыкновенными дробями лишь эпизодически, они
использовали различные обозначения. Герон и Диофант, самые известные
арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем
числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с
единичным числителем, либо шестидесятеричным дробям.
Недостатки греческих обозначений дробных чисел, включая использование
шестидесятеричных дробей в десятичной системе счисления, объяснялись отнюдь не пороками
основополагающих принципов. Недостатки греческой системы счисления можно отнести скорее за счет
их упорного стремления к строгости, которое заметно увеличило трудности, связанные с анализом
отношения несоизмеримых величин. Слово “число” греки понимали как набор единиц, поэтому то, что
мы теперь рассматриваем как единое рациональное число – дробь, – греки понимали как отношение
двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой
арифметике. Кроме того, десятичные представления обыкновенных дробей в большинстве случаев
бесконечны. А поскольку бесконечность была исключена из строгих рассуждений, теоретическая
арифметика не нуждалась в такого рода представлениях. С другой стороны, областью, в которой
практические вычисления испытывали величайшую потребность в точных дробях, была астрономия, а
здесь вавилонская традиция была настолько сильна, что шестидесятеричная система обозначений
угловых, дуговых и временных величин сохраняется и поныне.
Рим
Римские обозначения чисел известны ныне лучше, чем любая другая древняя
система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы,
сколько тем огромным влиянием, которым пользовалась Римская империя в сравнительно недавнем
прошлом. Этруски, завоевавшие Римскую империю в 7 в. до н.э., испытали на себе влияние
восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов
римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах
счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся
символы. Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были,
соответственно, символы I, V, X, Q (или Å, или Ä) и f (или Хотя о первоначальном значении этих символов было написано много, их
удовлетворительного объяснения у нас нет до сих пор. Согласно одной из
распространенных теорий, римская цифра V изображает раскрытую руку с четырьмя
прижатыми друг к другу пальцами и отставленным большим пальцем; символ X,
согласно той же теории, изображает две скрещенные руки или сдвоенную цифру V.
Символы чисел 100 и 1000, возможно, берут начало от греческих букв Q и f.
Неизвестно, произошли ли более поздние обозначения C и M от старых римских
символов или они акрофонически связаны с начальными буквами латинских слов,
означавших 100 (центум) и 1000 (милле). Полагают, что римский символ числа 500,
буква D, возник из половинки старого символа, обозначавшего 1000. Если не
считать, что большинство римских символов скорее всего не были акрофоническими
и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями
символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления
напоминала аттическую. Разумеется, в деталях они отличались. Римляне часто
использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX и
XC вместо LXXXX; сравнительно позднее символ IV вместо IIII.
В целом римляне не были склонны заниматься
математикой, поэтому не испытывали особой потребности в больших числах. Тем не
менее для обозначения 10000 они эпизодически использовали символ Америка
Исследователи, путешествовавшие в 16 в. по Центральной Америке, обнаружили цивилизации с
высокоразвитыми системами счисления, отличными от тех, которые были известны в
Европе. Самыми важными элементами в системе счисления майя были использование
позиционного принципа и символа нуля. Если отвлечься от того, что принятая у
индейцев майя система счисления была не шестидесятеричной, а двадцатеричной и
вместо 10 использовала вспомогательное основание 5, то в остальном принципы
были аналогичны тем, которые ранее были в ходу у жителей Древнего Вавилона. В
схеме майя точка означала единицу, а повторяющиеся точки – числа до четырех;
пятерку обозначала горизонтальная черта, а две и три горизонтальные черты
обозначали, соответственно, числа десять и пятнадцать. Для обозначения числа
двадцать майя воспользовались позиционным принципом, используя точку,
помещенную над символом нуля. (Последний имел вид
Индия
Письменных памятников древнеиндийской цивилизации сохранилось очень немного,
но, судя по всему, индийские системы счисления проходили в своем развитии те же этапы, что
и во всех прочих цивилизациях. На древних надписях из Мохенджо-Даро
вертикальная черточка в записи чисел повторяется до тринадцати раз, а
группировка символов напоминает ту, которая знакома нам по египетским
иероглифическим надписям. В течение некоторого времени имела хождение система
счисления, очень напоминающая аттическую, в которой для обозначения чисел 4,
10, 20 и 100 использовались повторения коллективных символов. Эта система, которая
называется кхарошти, постепенно уступила место другой, известной под названием
брахми, где буквами алфавита обозначались единицы (начиная с четырех), десятки,
сотни и тысячи. Переход от кхарошти к брахми происходил в те годы, когда в
Греции, вскоре после вторжения в Индию Александра Македонского, ионическая
система счисления вытеснила аттическую. Вполне возможно, что переход от
кхарошти к брахми происходил под влиянием греков, но сейчас вряд ли возможно
хоть как-то проследить или восстановить этот переход от древних индийских форм
к системе, от которой произошли наши системы счисления. Надписи, найденные в
Нана-Гат и Насике, относящиеся к первым векам до нашей эры и первым векам нашей
эры, по-видимому, содержат обозначения чисел, которые были прямыми предшественниками
тех, которые получили теперь название индо-арабской системы. Первоначально в
этой системе не было ни позиционного принципа, ни символа нуля. Оба эти
элементы вошли в индийскую систему к 8–9 вв. вместе с обозначениями деванагари
(см. таблицу обозначений чисел). В индийской системе число 6789 записывалось бы
Напомним, что позиционная система счисления с
нулем возникла не в Индии. За много веков до этого она использовалась
в Древнем Вавилоне с шестидесятеричной системой. Поскольку индийские
астрономы использовали шестидесятеричные дроби, вполне возможно, что это навело
их на мысль перенести позиционный принцип с шестидесятеричных дробей на целые
числа, записанные в десятичной системе. В итоге произошел сдвиг, приведший к
современной системе счисления. Не исключена также возможность, что такой
переход, по крайней мере отчасти, произошел в Греции, скорее всего в
Александрии, и оттуда распространился в Индию. В пользу последнего
предположения свидетельствует сходство кружка, обозначающего нуль, с
начертанием греческой буквы омикрон. Однако происхождение индийского символа
для нуля окутано тайной, так как первое достоверное свидетельство его появления
в Индии датируется лишь концом 9 в. Как ни странно, ни греки, ни индийцы не
включили в свои системы счисления десятичные дроби, но именно индийцам мы
обязаны современной системой записи обыкновенных дробей с числителем,
расположенным над знаменателем (но без горизонтальной черты, отделяющей
числитель от знаменателя).
Аравия
Современную
систему обозначения чисел часто называют арабской, хотя ясно, что она берет
начало не из Аравии. До хиджры арабы записывали числа словами, но затем, как
это делали ранее греки, они стали обозначать числа буквами своего алфавита. В
772 индийский трактат “Сидданта” был привезен в Багдад и переведен на арабский,
после чего стали использоваться две системы записи чисел: (1) в астрономии
по-прежнему употребляли алфавитную систему, (2) в торговых расчетах купцы стали
применять систему, заимствованную из Индии. Но даже среди тех, кто пользовался
индийской системой, начертания цифр, как и в Индии, сильно варьировали. Эти две
системы счисления были широко распространены и после распада арабского
халифата. В его восточной части пользовались системой, аналогичной той, которая
и сейчас встречается в арабском мире. Число 6789 в этой системе записывается
как Свое название эти обозначения получили потому, что ими пользовались при
вычислениях на “песчаном абаке”. Как свидетельствует Бируни, индийцы часто
производили вычисления на песке, что, возможно, и послужило поводом для такого
названия. Тем не менее само происхождение этих цифр, от которых в свою очередь
произошли наши современные цифры, остается неизвестным.
Западная Европа
Первым европейским
ученым, о котором достоверно известно, что он ввел в употребление в Европе
арабские цифры, был Герберт, работавший в Испании и позднее (в 999-м) ставший
папой Сильвестром II.
В 12 в. Хуан из Севильи перевел на латынь трактат De
numero indorum (Об индийских числах) арабского математика Аль-Хорезми. Когда в
следующем веке индийские обозначения стали широко известными, новая система
получила название алгоритм – от искаженного Аль-Хорезми. Через пару столетий
европейские алгоритмики одержали верх и над абацистами, и над теми, кто
пользовался римскими цифрами в вычислениях с целыми числами, но лишь с 1585
индо-арабская система обозначений, систематически расширяясь, стала
использоваться и применительно к дробям. В том же году Симон Стевин опубликовал
свой небольшой трактат De Thiende (Десятина), в котором он предложил записывать
в виде ![]() 2. Обозначения чисел и история систем счисления
2. Обозначения чисел и история систем счисления

 вместо
вместо  , а семьсот как
, а семьсот как
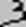 вместо
вместо 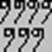 . В этой записи число 6789 имело вид
. В этой записи число 6789 имело вид
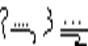 , причем знаки более высокого порядка располагались справа, а не слева.
Иероглифическая запись чисел использовалась преимущественно в официальных документах и текстах.
Еще позднее иератическая система обозначения чисел уступила место демотическим системам записи.
Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем
счисления, так как дало возможность существенно сократить записи. Однако их операции с дробями
продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. дроби
с числителем 1) и каждую дробь записывали в виде суммы аликвотных дробей, например, дробь 2/43
они записали бы так: 1/42 + 1/86 + 1/129 + 1/301. В этих системах счисления над символом,
обозначающим знаменатель, ставился специальный знак. В искусстве оперирования дробями египтяне
значительно уступали жителям Месопотамии.
, причем знаки более высокого порядка располагались справа, а не слева.
Иероглифическая запись чисел использовалась преимущественно в официальных документах и текстах.
Еще позднее иератическая система обозначения чисел уступила место демотическим системам записи.
Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем
счисления, так как дало возможность существенно сократить записи. Однако их операции с дробями
продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. дроби
с числителем 1) и каждую дробь записывали в виде суммы аликвотных дробей, например, дробь 2/43
они записали бы так: 1/42 + 1/86 + 1/129 + 1/301. В этих системах счисления над символом,
обозначающим знаменатель, ставился специальный знак. В искусстве оперирования дробями египтяне
значительно уступали жителям Месопотамии.
 (в раннешумерских текстах – небольшой кружок).
(в раннешумерских текстах – небольшой кружок).
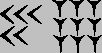 , т.е. 5×10+9.
, т.е. 5×10+9.
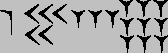 т.е. 1×(60)2 + 53×(60) + 9.
В Древнем Вавилоне, ок. 1650 до н.э., система счисления оставалась псевдопозиционной
или лишь относительно позиционной, поскольку не существовало эквивалента современной десятичной
запятой, равно как и символа для обозначения отсутствующей позиции. Обозначал
ли символ
т.е. 1×(60)2 + 53×(60) + 9.
В Древнем Вавилоне, ок. 1650 до н.э., система счисления оставалась псевдопозиционной
или лишь относительно позиционной, поскольку не существовало эквивалента современной десятичной
запятой, равно как и символа для обозначения отсутствующей позиции. Обозначал
ли символ  число
1×(60)2 + 1 или 1×(60)2 + 1×(60),
приходилось догадываться из контекста. Однако в период правления селевкидов,
ок. 300 до н.э., эта неоднозначность была устранена введением специального
символа в виде двух небольших клиньев, помещаемого на пустующее место, т.е.
обозначающего пустую позицию в записи числа. Таким образом, из системы
счисления была устранена отмеченная выше неоднозначность. Например, символ
число
1×(60)2 + 1 или 1×(60)2 + 1×(60),
приходилось догадываться из контекста. Однако в период правления селевкидов,
ок. 300 до н.э., эта неоднозначность была устранена введением специального
символа в виде двух небольших клиньев, помещаемого на пустующее место, т.е.
обозначающего пустую позицию в записи числа. Таким образом, из системы
счисления была устранена отмеченная выше неоднозначность. Например, символ
 означал
число 3601, т.е. 1×(60)2 + 0×(60) + 1. В то же время не
было найдено ни одной таблички с записью, в которой символ нуля находился бы в
конце числа. Именно поэтому вавилонскую систему мы считаем лишь относительно
позиционной, ибо самый правый знак мог означать либо единицы, либо кратные
какой-нибудь степени числа 60. Тем не менее изобретение вавилонянами
позиционной системы счисления с нулем представляло собой огромное достижение,
по своему революционному значению для математики сопоставимое разве лишь с
более поздней гипотезой Коперника в астрономии.
означал
число 3601, т.е. 1×(60)2 + 0×(60) + 1. В то же время не
было найдено ни одной таблички с записью, в которой символ нуля находился бы в
конце числа. Именно поэтому вавилонскую систему мы считаем лишь относительно
позиционной, ибо самый правый знак мог означать либо единицы, либо кратные
какой-нибудь степени числа 60. Тем не менее изобретение вавилонянами
позиционной системы счисления с нулем представляло собой огромное достижение,
по своему революционному значению для математики сопоставимое разве лишь с
более поздней гипотезой Коперника в астрономии.
 , 500 – символом
, 500 – символом  ,
5000 – символом
,
5000 – символом  , 50000 – символом
, 50000 – символом  .
Еще большие числа обычно описывались словами. Число 6789 в аттической системе записывалось в виде
.
Еще большие числа обычно описывались словами. Число 6789 в аттической системе записывалось в виде
 .
.
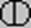 ,
или
,
или 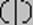 ).
).
 ,
а для числа 100000 – символ
,
а для числа 100000 – символ  . Половинки этих символов иногда
использовались для обозначения чисел 5000 (
. Половинки этих символов иногда
использовались для обозначения чисел 5000 (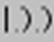 )
и 50000 (
)
и 50000 (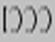 ). Таким образом, в римских обозначениях число 6789 можно
было бы записать как
). Таким образом, в римских обозначениях число 6789 можно
было бы записать как 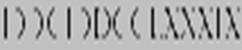 .
.
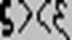 .
Здесь мы впервые встречаемся с элементами современной системы счисления: индийская
система была десятичной, цифровой и позиционной. При желании можно даже
усмотреть некоторое сходство в начертании современных цифр и цифр деванагари.
.
Здесь мы впервые встречаемся с элементами современной системы счисления: индийская
система была десятичной, цифровой и позиционной. При желании можно даже
усмотреть некоторое сходство в начертании современных цифр и цифр деванагари.
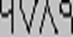 .
Однако обозначения чисел в Испании 10 в. настолько сильно отличались по своим
начертаниям от приведенных выше, что казались никак с ними не связанными. В
испанских обозначениях, получивших название “гобар” или “песчаных”, число 6789
выглядело бы так:
.
Однако обозначения чисел в Испании 10 в. настолько сильно отличались по своим
начертаниям от приведенных выше, что казались никак с ними не связанными. В
испанских обозначениях, получивших название “гобар” или “песчаных”, число 6789
выглядело бы так:  .
.
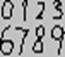 или
или 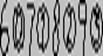 число,
которое мы записали бы как 6789. В 17 в. вошла в употребление десятичная
запятая (или точка), которой стали отделять целую часть числа от дробной, после
чего европейцы отказались от предложенной Стевином индексации разрядов. После
этих изменений развитие современной системы счисления завершилось. (Это отнюдь
не означает, будто была достигнута полная стандартизация в названиях или
обозначениях чисел. В Америке и Франции биллион означает тысячу миллионов, а в
Англии и Германии – миллион миллионов; в континентальной Европе часто
используется десятичная запятая, а в англосаксонских странах предпочитают
ставить десятичную точку; англосаксы используют запятые, чтобы отделять степени
тысячи, в некоторых странах для этой цели служит точка.
число,
которое мы записали бы как 6789. В 17 в. вошла в употребление десятичная
запятая (или точка), которой стали отделять целую часть числа от дробной, после
чего европейцы отказались от предложенной Стевином индексации разрядов. После
этих изменений развитие современной системы счисления завершилось. (Это отнюдь
не означает, будто была достигнута полная стандартизация в названиях или
обозначениях чисел. В Америке и Франции биллион означает тысячу миллионов, а в
Англии и Германии – миллион миллионов; в континентальной Европе часто
используется десятичная запятая, а в англосаксонских странах предпочитают
ставить десятичную точку; англосаксы используют запятые, чтобы отделять степени
тысячи, в некоторых странах для этой цели служит точка.