5. Основы тензорного анализа
 5.16. Алгебра тензоров общего вида
5.16. Алгебра тензоров общего вида 
В настоящем разделе будут приведены основные правила выполнения действий с тензорами общего
вида, которые определяются согласно (
325), при этом соответствующие доказательства
будут опущены, поскольку они во многом подобны уже рассмотренным выше для "простых" тензоров
и могут служить хорошим упражнением для читателя.
а)
сложение тензоров: суммой тензоров
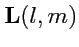
и
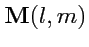
называется новый тензор
такого же ранга и обозначаемый как
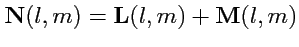
с координатами:
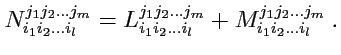 |
(326) |
Например, сложение двух контравариантных тензоров 1-го ранга
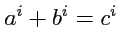
соответствует сложению
векторов

, а ковариантных
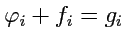
- сложению двух функций от векторов
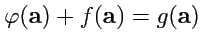
. Отметим, что сложение тензоров коммутативно;
б) умножение тензоров: правило умножения тензоров можно записать в форме
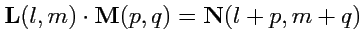 |
(327) |
или в координатах
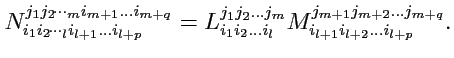 |
(328) |
Произведение тензоров в общем случае некоммутативно, так как в определение этого действия входит
способ нумерации координат тензоров с помощью индексов.
Пример 5-1. Рассмотрим выражение
которое, согласно (
328), является тензором второго ранга. С другой стороны тензор

определяет линейный оператор
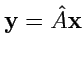
, т. е.
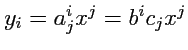
. Но
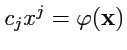
- линейная функция. Таким образом, действие оператора
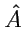
, который
равен произведению ковариантного и контравариантного тензоров,равно
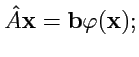 |
(329) |
в)
свертка: как и раньше, указанная операция позволяет строить новые тензоры с помощью
суммирования координат, которое "объединяет" выбранные пары индексов, в которых, учитывая свойства
рассматриваемых тензоров, один индекс должен быть верхним, а второй (обязательно) - нижним. Например,
из тензора
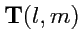
ранга

можно построить новый тензор
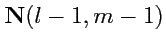
следующим
образом:
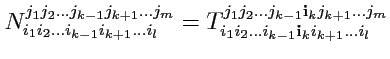 |
(330) |
при этом ранг тензора понижается на 2;
г) подстановка индексов: в определение оператора входит положение ковариантных и контравариантных
индексов. Поэтому, если переставить местами пары ковариантных или контравариантных индексов (но не
ковариантного с контравариантным !), то получится новый тензор
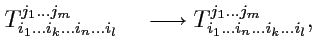 |
(331) |
а указанное действие называется подстановкой индексов. При подстановке структура нового тензора не
меняется, т. е. в выбранном базисе набор координат будет таким же, но "принадлежать" эти координаты
будут другим базисным векторам, определяя, таким образом, новый тензор. Сама по себе операция подстановки
индексов малосодержательна и ее основное значение сказывается в операциях, где она комбинируется со
сложением, особенно при
симметрировании и
альтерации. При симметрировании новый тензор
получается как результат усреднения координат тензора, соответствующих всевозможным перестановкам
из выбранных
индексов общим числом
. Обозначается симметрирование круглыми скобками, которые
заключают выбранные индексы. Например, для симметрирования по 2-м индексам
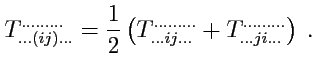 |
(332) |
При симметрировании по трем индексам имеем (
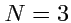
,
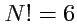
):
![\begin{displaymath}\begin{array}{ccc} T_{\dots(ijk)\dots}^{\dots\dots\dots} &=&\...
...T_{\dots(kji)\dots}^{\dots\dots\dots} \biggr]\ . \\ \end{array}\end{displaymath}](img1296.png) |
(333) |
Как видно из определения и приведенных примеров, операция симметрирования позволяет получать симметричные
тензоры, свойства которых были рассмотрены ранее.
Операция альтерирования, которая обозначается квадратными скобками, подобна симметрированию, но координаты
тензора при этом дополнительно умножаются на

, где
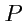
- четность перестановки индексов. Например,
![$\displaystyle T_{\dots[ij]\dots}^{\dots\dots\dots} = \displaystyle{\frac{1}{2}}...
...\dots ij\dots}^{\dots\dots\dots} - T_{\dots ji\dots}^{\dots\dots\dots} \right).$](img1299.png) |
(334) |
Операция альтерирования позволяет, таким образом, получать тензоры антисимметричные или
кососимметричные по индексам, участвовавшим в альтерации. Отметим очевидное свойство:
если
![$ A_{\dots ij\dots}^{\dots\dots\dots} = T_{\dots[ij]\dots}^{\dots\dots\dots}$](img1300.png)
, то
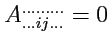
и в том числе для любого числа альтерированных индексов.
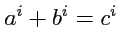 соответствует сложению
векторов
соответствует сложению
векторов
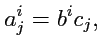
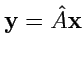 , т. е.
, т. е.
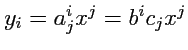 . Но
. Но
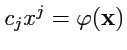 - линейная функция. Таким образом, действие оператора
- линейная функция. Таким образом, действие оператора  , где
, где