4. Векторный анализ в криволинейных координатах
 4.1. Криволинейные системы координат
4.1. Криволинейные системы координат 
Как видно из предыдущего рассмотрения, определение понятия поля (скалярного, векторного),
основных дифференциальных операций и характеристик полей было дано безотносительно к
координатной системе. Однако, при решении конкретных задач приходится, тем не менее, использовать
систему координат. При этом, в простейшем случае положение некоторой точки
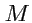
в пространстве
задавалось с помощью тройки чисел
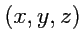
так, что радиус-вектор (бескоординатное определение
положения) представлялся в виде разложения по неподвижному декартовому ортонормированному
базису
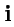
,
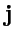
,
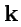
с началом в фиксированной точке
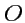
в виде:
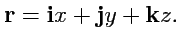 |
(183) |
Тройка чисел
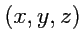
называется прямоугольными декартовыми координатами точки
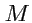
. Использование
координат, таким образом, просто означает способ нумерации точек пространства и декартовая система
координат в этом смысле не является уникальной. Кроме того, несмотря на свою простоту, эта система
может сильно затруднить решение некоторых задач, требующих использования координатных систем.
Поэтому во многих случаях бывает удобно определять положение точки в пространстве не числами
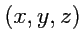
, а какими-нибудь другими
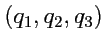
.
Числа
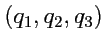
называются
криволинейными координатами точки. Тогда,
радиус-вектор точки
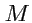
должен быть, как и в случае декартовой системы координат, функцией
криволинейных координат, т. е.
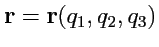
или в проекциях на декартовые оси
координат
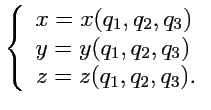 |
(184) |
С другой стороны, задание тройки
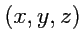
также определяет положение точки в пространстве,
поэтому ее криволинейные координаты должны быть функциями декартовых:
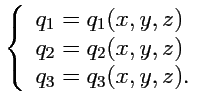 |
(185) |
Если рассматривать (
184) как систему уравнений, то из математического анализа известно,
что ее решение, т. е. (
185), можно получить в случае, если определитель (якобиан):
![$\displaystyle \displaystyle{\frac{\partial (x,y,z)}{\partial (q_1,q_2,q_3)}} = ...
...splaystyle{\frac{\partial z}{\partial q_3}}\ \\ [1.0em] \end{array} \right\vert$](img873.png) |
(186) |
будет отличен от нуля. В дальнейшем будем предполагать, что обратное также выполняется:
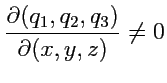 |
(187) |
и вместе (
186)-(
187) будут, таким образом, определять связь между декартовыми
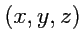
и криволинейными
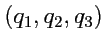
координатами.
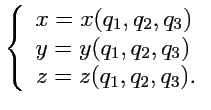
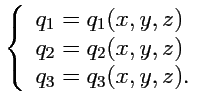
![$\displaystyle \displaystyle{\frac{\partial (x,y,z)}{\partial (q_1,q_2,q_3)}} = ...
...splaystyle{\frac{\partial z}{\partial q_3}}\ \\ [1.0em] \end{array} \right\vert$](img873.png)