Задачи для самостоятельной работы

I. Найти поток векторного поля ${\mathbf A}({\mathbf r})$ через замкнутую поверхность $\Sigma$ , используя теорему Остроградского-Гаусса для векторных полей:

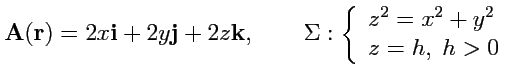
1. ${\mathbf A}({\mathbf r})=2x{\mathbf i}+2y{\mathbf j} + 2z{\mathbf k},\qquad\Sigma: \left\{\begin{array}{l} z^2=x^2+y^2 \\ z=h,\; h>0 \\ \end{array}\right.$

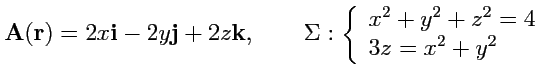
2. ${\mathbf A}({\mathbf r})=2x{\mathbf i}-2y{\mathbf j} + 2z{\mathbf k},\qquad\Sigma: \left\{\begin{array}{l} x^2+y^2+z^2=4 \\ 3z=x^2+y^2 \\ \end{array}\right.$

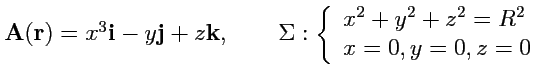
2. ${\mathbf A}({\mathbf r})=x^3{\mathbf i}-y{\mathbf j} + z{\mathbf k},\qquad\Sig... ...left\{\begin{array}{l} x^2+y^2+z^2=R^2 \\ x=0, y=0, z=0 \\ \end{array}\right.$

II. Вычислить циркуляцию векторного поля ${\mathbf A}({\mathbf r})$ по контуру , используя теорему Стокса для векторных полей:

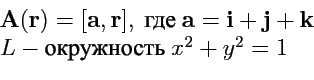
1. $\begin{displaymath}\begin{array}{l} {\mathbf A}({\mathbf r}) = [{\mathbf a},{\m... ...mathbf k}\\ L - \mbox{окружность}\ x^2+y^2=1\\ \end{array} \end{displaymath}$

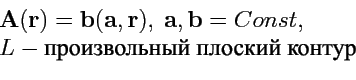
2. $\begin{displaymath}\begin{array}{l} {\mathbf A}({\mathbf r}) ={\mathbf b}({\mat... ...Const,\\ L - \mbox{произвольный плоский контур} \end{array} \end{displaymath}$

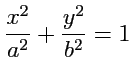
3. ${\mathbf A}({\mathbf r})={\mathbf r}$ , - эллипс $\displaystyle{\frac{x^2}{a^2}}+\displaystyle{\frac{y^2}{b^2}}=1$

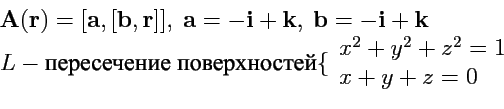
4. $\begin{displaymath}\begin{array}{l} {\mathbf A}({\mathbf r})=[{\mathbf a},[{\ma... ...rray}{l} x^2+y^2+z^2=1\\ x+y+z=0 \end{array} \end{array} \end{displaymath}$

III. Показать, что поле ${\mathbf A}({\mathbf r})$ является потенциальным:

1. ${\mathbf A}({\mathbf r})=(y+z){\mathbf i} + (x+z){\mathbf j} + (x+y){\mathbf k}$

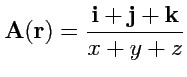
2. ${\mathbf A}({\mathbf r})=\displaystyle{\frac{{\mathbf i}+{\mathbf j}+{\mathbf k}}{x+y+z}}$

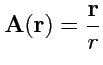
3. ${\mathbf A}({\mathbf r})=\displaystyle{\frac{{\mathbf r}}{r}}$

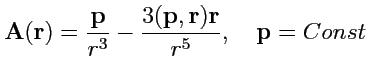
4. ${\mathbf A}({\mathbf r})=\displaystyle{\frac{{\mathbf p}}{r^3}}-\displaystyle{\frac{3({\mathbf p},{\mathbf r}){\mathbf r}}{r^5}},\quad {\mathbf p}=Const$
IV. Показать, что поле ${\mathbf A}({\mathbf r})$ является соленоидальным:

1. ${\mathbf A}({\mathbf r})=2y{\mathbf i}-z{\mathbf j}+2x{\mathbf k}$

2. ${\mathbf A}({\mathbf r})={\mathbf i}+{\mathbf j}+{\mathbf k}$

3. ${\mathbf A}({\mathbf r})=2y{\mathbf i}+2z{\mathbf j}$

4. ${\mathbf A}({\mathbf r})=(z-y){\mathbf i} + (x-z){\mathbf j} + (y-x){\mathbf k}$

V. Вычислить ( ${\mathbf a}$ - постоянный вектор)

1.	${\rm grad}\,r^n$	7.	${\rm div}\,{\mathbf a}r^n$
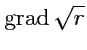2.	${\rm grad}\,\sqrt{r}$	8.	${\rm div}\,{\mathbf r}\ln(r)$
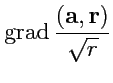3.	${\rm grad}\,\displaystyle{\frac{({\mathbf a},{\mathbf r})}{\sqrt{r}}}$	9.	${\rm div}\,r^3{\mathbf r}$