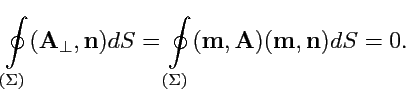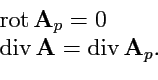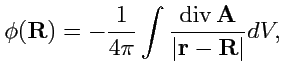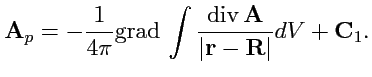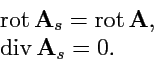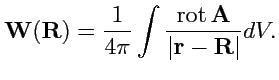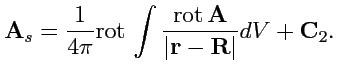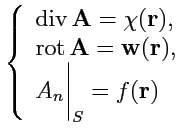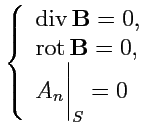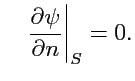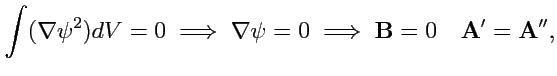3. Дифференциальные характеристики полей

Специальные векторные поля 3.13. Основная теорема векторного анализа. Нахождение поля по его дивергенции и ротору Задачи для самостоятельной работы


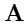
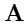
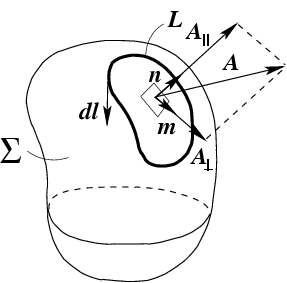
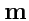
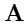
Рассмотрим произвольное векторное поле $ {\mathbf A}$. Выберем в пространстве, где определено поле $ {\mathbf A}$, некоторую замкнутую поверхность $ \Sigma$ (рис. 33). Пусть $ {\mathbf n}$ - нормаль к $ \Sigma$, а $ {\mathbf m}$ - единичный, касательный к $ \Sigma$ вектор, т. е. $ ({\mathbf n},{\mathbf m})=0$. Тогда поле $ {\mathbf A}$можно представить в виде
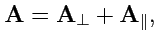$\displaystyle {\mathbf A}={\mathbf A}_\perp + {\mathbf A}_\parallel,$ (163)
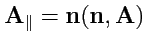
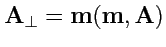
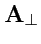
где $ {\mathbf A}_\parallel={\mathbf n}({\mathbf n},{\mathbf A})$, $ {\mathbf A}_\perp={\mathbf m}({\mathbf m},{\mathbf A})$. Рассмотрим поток поля $ {\mathbf A}_\perp$ через поверхность $ \Sigma$:
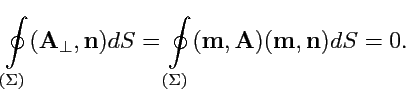$\displaystyle \oint\limits_{(\Sigma)}({\mathbf A}_\perp,{\mathbf n})dS = \oint\limits_{(\Sigma)}({\mathbf m},{\mathbf A})({\mathbf m},{\mathbf n})dS=0.$ (164)
Тогда по теореме Остроградского-Гаусса для векторных полей получим:

Рис.33 Разложение векторного поля

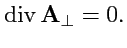$\displaystyle {\rm div}\,{\mathbf A}_\perp = 0.$ (165)
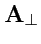
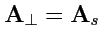
Согласно (156) поле $ {\mathbf A}_\perp$ является соленоидальным, $ {\mathbf A}_\perp={\mathbf A}_s$.
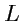
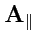
      Аналогично, если $ L$ - замкнутый контур на поверхности $ \Sigma$, то циркуляция поля $ {\mathbf A}_\parallel$
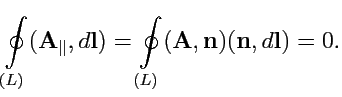$\displaystyle \oint\limits_{(L)}({\mathbf A}_\parallel,d{\mathbf l}) = \oint\limits_{(L)}({\mathbf A},{\mathbf n})({\mathbf n},d{\mathbf l}) = 0.$ (166)
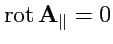
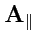
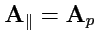
и тогда из теоремы Стокса для векторных полей следует, что $ {\rm rot}\,{\mathbf A}_\parallel=0$, т. е. поле $ {\mathbf A}_\parallel$ является потенциальным, $ {\mathbf A}_\parallel={\mathbf A}_p$. Таким образом, произвольное векторное поле можно представить в виде
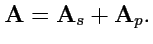$\displaystyle {\mathbf A}={\mathbf A}_s + {\mathbf A}_p.$ (167)

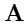
      Если векторное поле $ {\mathbf A}$ удовлетворяет определенным требованиям, то (167) может быть доказано в общем виде и имеет место
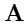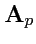      ТЕОРЕМА: любое векторное поле $ {\mathbf A}$, заданное во всем пространстве и убывающее до нуля на бесконечности вместе со своими ротором и дивергенцией, может быть единственным образом представлено в виде суммы потенциального $ {\mathbf A}_p$ и соленоидального 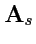$ {\mathbf A}_s$ полей.
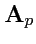
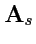
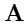
      Доказательство. Построим поля $ {\mathbf A}_p$ и $ {\mathbf A}_s$ по заданному полю $ {\mathbf A}$. Из условия теоремы следует:
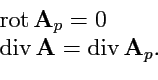\begin{displaymath}\begin{array}{l} {\rm rot}\,{\mathbf A}_p = 0\\ {\rm div}\,{\mathbf A} = {\rm div}\,{\mathbf A}_p. \end{array}\end{displaymath} (168)
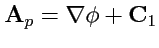
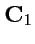
Потенциальное поле - поле градиента, т. е. $ {\mathbf A}_p = \nabla\phi+{\mathbf C}_1$, где $ {\mathbf C}_1$ - векторная константа. Тогда из (134) и (168)
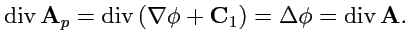$\displaystyle {\rm div}\,{\mathbf A}_p = {\rm div}\,(\nabla\phi + {\mathbf C}_1) = \Delta\phi = {\rm div}\,{\mathbf A}.$ (169)
Используя следствие из 2-ой формулы Грина (148) и устремляя поверхность на бесконечность, где, согласно условию теоремы, поле исчезает, получим
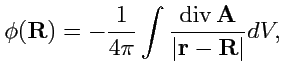$\displaystyle \phi({\mathbf R}) = -\displaystyle{\frac{1}{4\pi}}\int\displaystyle{\frac{{\rm div}\,{\mathbf A}}{\vert{\mathbf r}-{\mathbf R}\vert}}dV,$ (170)
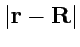
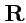
где $ \vert{\mathbf r}-{\mathbf R}\vert$ - расстояние от текущей точки в подинтегральном выражении до точки $ {\mathbf R}$, в которой определяется поле $ \phi$. Из (170) получается:
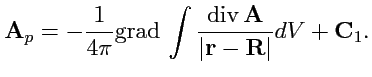$\displaystyle {\mathbf A}_p = -\displaystyle{\frac{1}{4\pi}}{\rm grad}\,\int\di... ...{{\rm div}\,{\mathbf A}}{\vert{\mathbf r}-{\mathbf R}\vert}}dV + {\mathbf C}_1.$ (171)

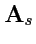
Аналогично для поля $ {\mathbf A}_s$:
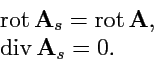\begin{displaymath}\begin{array}{l} {\rm rot}\,{\mathbf A}_s = {\rm rot}\,{\mathbf A},\\ {\rm div}\,{\mathbf A}_s = 0. \end{array}\end{displaymath} (172)
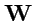
Соленоидальное поле может быть представлено, как ротор векторного потенциала, $ {\mathbf A}_s={\rm rot}\,{\mathbf W}+{\mathbf C}_s$. Так как векторный потенциал определен с точностью до градиента некоторой функции (158), то $ {\mathbf W}$ можно выбрать так, чтобы выполнялось условие
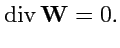$\displaystyle {\rm div}\,{\mathbf W}=0.$ (173)
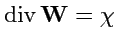
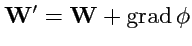
Действительно, если (173) не выполняется и $ {\rm div}\,{\mathbf W}=\chi$, то построим новое поле $ {\mathbf W}'={\mathbf W}+{\rm grad}\,\phi$ так, чтобы (173) выполнялось
$\displaystyle {\rm div}\,{\mathbf W}'={\rm div}\,({\mathbf W}+{\rm grad}\,\phi) = \chi + \Delta\phi = 0. $
Тогда, $ \phi$ можно определить из уравнения Лапласа
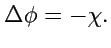$\displaystyle \Delta\phi = -\chi.$ (174)
С учетом (138), (173) из (157), получим:
$\displaystyle {\rm rot}\,{\mathbf A}_s = {\rm rot}\,({\mathbf W}+{\mathbf C}_s)... ...grad}\,{\rm div}\,{\mathbf W} - \Delta{\mathbf W} = {\rm rot}\,{\mathbf A},\\ $
или
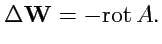$\displaystyle \Delta{\mathbf W} = -{\rm rot}\,{A}.$ (175)
Уравнение (175) аналогично (169) и тогда
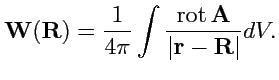$\displaystyle {\mathbf W}({\mathbf R}) = \displaystyle{\frac{1}{4\pi}}\int\displaystyle{\frac{{\rm rot}\,{\mathbf A}}{\vert{\mathbf r}-{\mathbf R}\vert}}dV.$ (176)
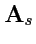
В (176) поверхностный интеграл также исчезает, если устремить поверхность на бесконечность. Тогда для поля $ {\mathbf A}_s$
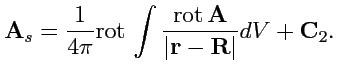$\displaystyle {\mathbf A}_s = \displaystyle{\frac{1}{4\pi}}{\rm rot}\,\int\disp... ...{{\rm rot}\,{\mathbf A}}{\vert{\mathbf r}-{\mathbf R}\vert}}dV + {\mathbf C}_2.$ (177)
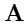
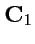
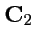
Так как по условию теоремы поле $ {\mathbf A}$ на бесконечности должно исчезать, то постоянные $ {\mathbf C}_1$ и $ {\mathbf C}_2$ должны быть равны нулю и окончательно имеем
$\displaystyle {\mathbf A}({\mathbf R}) = {\mathbf A}_p = -\displaystyle{\frac{1... ...splaystyle{\frac{{\rm rot}\,{\mathbf A}}{\vert{\mathbf r}-{\mathbf R}\vert}}dV,$ (178)
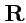
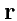
что доказывает теорему. Отметим, что "внешнее" дифференцирование выполняется по координатам вектора $ {\mathbf R}$, а интегрирование - по $ {\mathbf r}$.

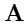
      Чтобы доказать однозначность разложения (178), учтем, что (178) с другой стороны означает, что векторное поле $ {\mathbf A}$ определяется заданием своих дивергенции и ротора. Тогда требование однозначности представления (178) означает, что система уравнений
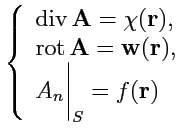$\displaystyle \left\{ \begin{array}{l} {\rm div}\,{\mathbf A} = \chi({\mathbf r... ...athbf w}({\mathbf r}),\\ A_n\biggr\vert _S = f({\mathbf r}) \end{array} \right.$ (179)
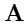
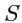
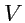
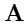
должна иметь единственное решение. В (179) последнее уравнение означает условие для нормальной составляющей поля $ {\mathbf A}$ на поверхности $ S$, ограничивающей объем $ V$, где задано поле $ {\mathbf A}$.
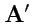
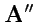
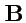
      Пусть (179) имеет два решения $ {\mathbf A}'$ и $ {\mathbf A}''$. Построим поле $ {\mathbf B}={\mathbf A}'-{\mathbf A}''$. (179) означает, что поле $ {\mathbf B}$ удовлетворяет системе уравнений
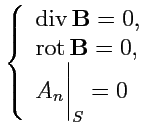$\displaystyle \left\{ \begin{array}{l} {\rm div}\,{\mathbf B} = 0, \\ {\rm rot}\,{\mathbf B} = 0, \\ A_n\biggr\vert _S = 0 \end{array} \right.$ (180)
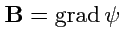
и следовательно может быть представлено в виде $ {\mathbf B}={\rm grad}\,\psi$. Тогда,
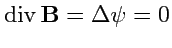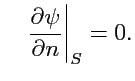$\displaystyle {\rm div}\,{\mathbf B} = \Delta\psi = 0$   и$\displaystyle \quad \displaystyle{\frac{\partial \psi}{\partial n}}\biggr\vert _S=0.$ (181)
Используя следствие (143) из 1-ой формулы Грина из (181), получим
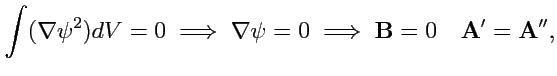$\displaystyle \int(\nabla\psi^2)dV = 0\;\Longrightarrow\; \nabla\psi=0\; \Longrightarrow\; {\mathbf B}=0 \quad {\mathbf A}'={\mathbf A}'',$ (182)
т. е. решение системы (179) единственно и, следовательно, представление произвольного векторного поля в виде (167) является однозначным.
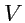
В заключение отметим, что с небольшими изменениями основная теорема векторного анализа может быть доказана для поля, заданного внутри конечного объема $ V$, ограниченного поверхностью $ \Sigma$, на которой известны нормальные составляющие этого поля.

Скалярные и векторные поля Векторный анализ в криволинейных координатах
Специальные векторные поля   Содержание   Задачи для самостоятельной работы