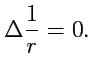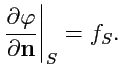3. Дифференциальные характеристики полей

Примеры решения задач 3.11. Следствия из интегральных теорем - формулы Грина Специальные вектореы поля


С помощью теоремы Остроградского-Гаусса (95) можно получить ряд полезных выражений, которые в математической физике носят название формул Грина.
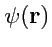
Рассмотрим две скалярные функции $ \varphi({\mathbf r})$ и $ \psi({\mathbf r})$, непрерывные вместе со своими первыми и вторыми частными производными.
1. Построим вектор $ {\mathbf A}=\varphi\nabla\psi$. Тогда
$\displaystyle {\rm div}\,{\mathbf A}=\varphi\Delta\psi + (\nabla\varphi,\nabla\psi) $

$\displaystyle ({\mathbf A},{\mathbf n})=(\varphi\nabla\psi,{\mathbf n})=\varphi... ...i,{\mathbf n})=\varphi\displaystyle{\frac{\partial \psi}{\partial {\mathbf n}}}$   из (81)$\displaystyle .$

Используя теорему Остроградского-Гаусса для векторных полей (95), получим

$\displaystyle \int\limits_{(V)}\left[\varphi\Delta\psi + (\nabla\varphi,\nabla\... ...\Sigma)}\varphi\displaystyle{\frac{\partial \psi}{\partial {\mathbf n}}}\ dS\ .$ (140)

(140) называется первой формулой Грина. Переписанная в виде

$\displaystyle \int\limits_{(V)} \varphi\Delta\psi\ dV = \oint\limits_{(\Sigma)}... ...{\partial {\mathbf n}}}\ dS - \int\limits_{(V)} (\nabla\varphi,\nabla\psi)\ dV,$ (141)

первая формула Грина является трехмерным аналогом формулы интегрирования по частям в математическом анализе.

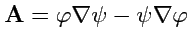
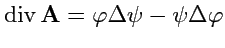
2. Построим вектор $ {\mathbf A}=\varphi\nabla\psi-\psi\nabla\varphi$. $ {\rm div}\,{\mathbf A}=\varphi\Delta\psi-\psi\Delta\varphi$. Используя теорему Остроградского-Гаусса, получим вторую формулу Грина:

$\displaystyle \int\limits_{(V)}\left[ \varphi\Delta\psi-\psi\Delta\varphi \righ... ... - \psi\displaystyle{\frac{\partial \varphi}{\partial {\mathbf n}}} \right]\ dS$ (142)

Частные случаи:

1. Если $ \varphi=\psi$, тогда из (140)

$\displaystyle \int\limits_{(V)}\left[\varphi\Delta\varphi + (\nabla\varphi)^2 \... ...Sigma)}\varphi\displaystyle{\frac{\partial \varphi}{\partial {\mathbf n}}}\ dS.$ (143)

2. $ \psi=$Const и из (142)

$\displaystyle \int\limits_{(V)}\Delta\varphi\ dV = \oint\limits_{(\Sigma)}\displaystyle{\frac{\partial \varphi}{\partial {\mathbf n}}}\ dS.$ (144)

Формулы Грина позволяют получить одно важное следствие. Рассмотрим в объеме $ V$, ограниченном поверхностью $ \Sigma$, непрерывную вместе со своими частными производными функцию $ \phi({\mathbf r})$. Тогда можно определить ее значение в любой точке $ M_0({\mathbf r}_0)$ объема $ V$, если известно значение $ \phi$ и ее производной в направлении нормали на поверхности $ \Sigma$ $ \displaystyle{\frac{\partial \phi}{\partial {\mathbf n}}}$ и значение $ \Delta\phi$ в каждой внутренней точке.

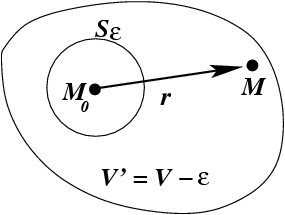
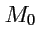
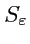
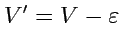
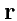
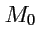
Для доказательства разобъем объем $ V$ на две области: сферическую $ \varepsilon $-окрестность точки $ M_0$, ограниченную сферой $ S_\varepsilon$ и остаток $ V'=V-\varepsilon$ (рис. 31). Пусть $ {\mathbf r}$ - вектор, проведенный из точки $ M_0$ в произвольную точку $ M$, принадлежащую объему $ V'$:

$\displaystyle r = \vert{\mathbf r}\vert=\sqrt{(x-x_0)^2+(y-y_0)^2+(z-z_0)^2}.$ (145)

Рис.31
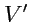
Прямым вычислением нетрудно проверить, что для любой точки $ M$ выполняется равенство
$\displaystyle \Delta\displaystyle{\frac{1}{r}} = 0. $
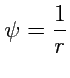
Пусть $ \psi=\displaystyle{\frac{1}{r}}$, тогда из второй формулы Грина (142) для объема $ V'$:

\begin{displaymath}\begin{array}{l} \displaystyle{ \int\limits_{(V')}-\displayst... ...al \varphi}{\partial {\mathbf n}}} \right]\ dS\ . } \end{array}\end{displaymath} (146)

Перейдем в (146) к пределу $ \varepsilon\to 0$ и учтем, что производная $ \displaystyle{\frac{\partial }{\partial {\mathbf n}}}\displaystyle{\frac{1}{r}... ...(\nabla\displaystyle{\frac{1}{r}},{\mathbf n}\right)=\displaystyle{\frac{1}{r}}$. По теореме о среднем
\begin{displaymath}\begin{array}{l} \displaystyle{ \lim_{\varepsilon\to 0}\oint\... ...repsilon} \right]\ 4\pi\rho^2 = 4\pi\varphi(M_0). } \end{array}\end{displaymath} (147)
Тогда из (146) с учетом (147), получим
$\displaystyle 4\pi\varphi(M_0) = -\int\limits_{(V)}\displaystyle{\frac{\Delta\v... ...1}{r}}\displaystyle{\frac{\partial \varphi}{\partial {\mathbf n}}} \right]\ dS,$ (148)
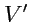
что и доказывает сформулированное выше утверждение. Отметим, что формула (148) фактически дает решение дифференциального уравнение (Пуассона)
$\displaystyle \Delta\varphi = 4\pi f({\mathbf r})$ (149)
с граничным условием
$\displaystyle \displaystyle{\frac{\partial \varphi}{\partial {\mathbf n}}}\biggr\vert _S=f_S. $


Скалярные и векторные поля Векторный анализ в криволинейных координатах
Примеры решения задач   Содержание   Специальные вектореы поля