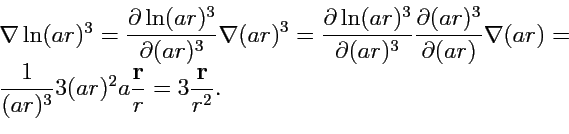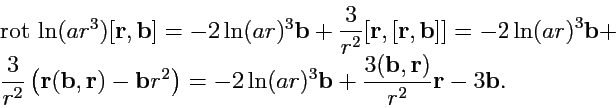3.
Дифференциальные характеристики полей
 3.10. Примеры решения задач на векторное дифференцирование
3.10. Примеры решения задач на векторное дифференцирование 
Так как для последнего слагаемого
![$ ({\mathbf b},\nabla)[{\mathbf r},{\mathbf a}]=-[{\mathbf a},{\mathbf b}]$](img726.png)
, то
Также можно использовать следующие преобразования и (
127) :
Наконец, координатный способ. Так как
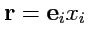
, то
Так как координаты радиус-вектора
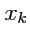
- независимые величины, то производная
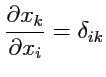
, тогда, используя свойство снятия сумм
для дельта-символа, получим
![$\displaystyle \nabla({\mathbf b},[{\mathbf r},{\mathbf a}]) = {\mathbf e}_i\dis...
...f e}_i\varepsilon_{jkl}b_ja_l\displaystyle{\frac{\partial x_k}{\partial x_i}}.
$](img730.png)
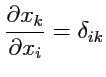 , тогда, используя свойство снятия сумм
для дельта-символа, получим
, тогда, используя свойство снятия сумм
для дельта-символа, получим
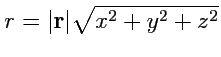 .
.![$\displaystyle {\rm rot}\,\ln(ar)^3[{\mathbf r},{\mathbf b}] = \ln(ar)^3{\rm rot}\,[{\mathbf r},{\mathbf b}] +
[\nabla\ln(ar)^3,[{\mathbf r},{\mathbf b}]].
$](img737.png)