Вычисление таких характеристик полей, как градиент, дивергенция и ротор заключается,
как уже было показано ранее, в вычислении соответствующих производных, их переменожении или
суммировании и, таким образом, представляет собой некоторое действие (операцию) над полем.
Общим свойством этой операции является ее векторный характер. Это свойство можно учесть
и в самой форме записи способа вычисления, если определить символический вектор -
оператор

(
набла):
который удовлетворяет всем правилам векторной алгебры, т. е. его можно умножать на число (скаляр)
или вектор. Знак

означает, что при этом соответствующая величина должна быть
подставлена сюда вместе с символом векторной операции. Тогда, сравнивая (
113) с
(
75), (
89) и (
112), получим:
Сравнивая далее (
114)-(
116) с (
79), (
92) и
(
106), получим, что в декартовой системе координат оператор

запишется как
Определение (
113) удобно тем, что оно пригодно для любой системы координат, в то
время как (
117) - частный случай для декартовой.
Оператор

является дифференциальным оператором а его действие, независимо от алгебраической
операции, в комбинации с которой он применяется к полю в (
114)-(
116),
подчиняется обычным правилам дифференцирования функций (сумма, произведение). В применении к
сложным выражениям, содержащим комбинации скалярных или векторных полей, вычисления градиента,
дивергенции или ротора на основе их определений может оказаться весьма громоздким, а при
использовании символической записи становится более наглядным и простым. При этом необходимо,
однако, следить, чтобы характер величин (скаляр или вектор) сохранялся на протяжении всех
вычислений, а каждое промежуточное выражение имело смысл с точки зрения векторной алгебры.
Например, если
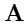
,
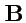
- векторы, то выражение
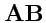
не имеет смысла, если
не указана сответствующая бинарная операции: сумма, скалярное или векторное произведение -
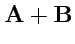
,
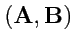
,
![$ [{\mathbf A},{\mathbf B}]$](img664.png)
.
Докажем формулы (
125) и (
123).
![$ {\rm rot}\,[{\mathbf A},{\mathbf B}]=[\nabla,[{\mathbf A},{\mathbf B}]]$](img674.png)
. Согласно правилу дифференцирования
произведения, будем отмечать те функции, которые будут оставаться постоянными, т. е.
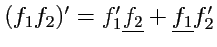
. Тогда:
Раскроем двойное векторное произведение по правилу
"BAC-
CAB", учитывая, что в первом слагаемом действию
дифференцирования "подвергается" вектор
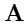
, во втором -
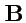
:
Во втором и четвертом слагаемых сомножители переставлены местами по свойству векторного
произведения, чтобы учесть предыдущие замечания. Опуская подчеркивания и переходя от
символической формы записи к соответствующим обозначениям, получим (
125).
Аналогично для (
123):
где были использованы свойства цикличности смешанного произведения векторов и антисимметрии
векторного. Остальные формулы предлагается доказать самостоятельно.
При выполнении векторного дифференцирования полезно знать следующие результаты для
простейших скалярных и векторных функций:
Формулы (
127) легко доказать с использованием определений градеинта, дивергенции
и ротора в декартовой системе координат.
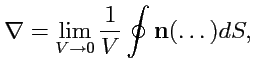
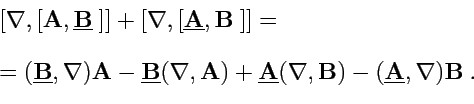
![\begin{displaymath}
\begin{array}{l}
{\rm div}\,[{\mathbf A},{\mathbf B}] = (\na...
...\mathbf A}) - ({\mathbf A},{\rm rot}\,{\mathbf B}),
\end{array}\end{displaymath}](img678.png)
![$\displaystyle \left. \begin{array}{lll} \mbox{1}. & \nabla r = \displaystyle{\f...
...pace{40mm}{\mathbf a}=\mbox{Const}, \\ [0.5em] \end{array} \right\}\hspace{0mm}$](img679.png)