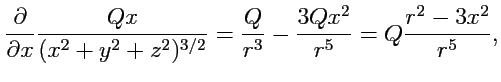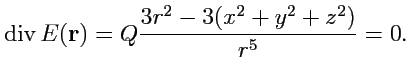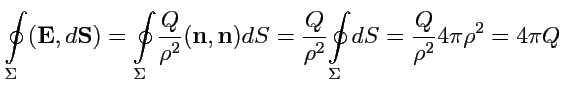3. Дифференциальные характеристики полей
 3.3. Поток векторного поля. Дивергенция
3.3. Поток векторного поля. Дивергенция 
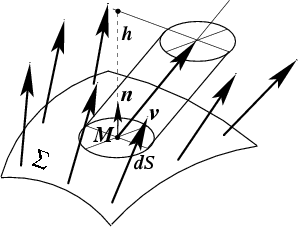
Понятие потока векторного поля можно определить на примере исследования скоростей течения
жидкости
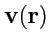
. Выберем в области поля
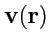
некоторую поверхность
произвольной формы (
рис.26).
Рис. 26 К определению потока векторного поля.
Так как поле задано во всех точках пространства,
окружающего эту поверхность, то вектор
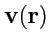
можно построить в любой точке

на поверхности. Рассмотрим площадку
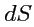
поверхности и вычислим количество жидкости,
протекающей через эту площадку за единицу времени. Эта величина будет равна плотности
жидкости
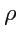
, умноженной на объем наклонного цилиндра с основанием
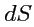
и образующей,
по модулю равной
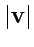
в точке

. Высота цилиндра равна проекции образующей на нормаль

в этой точке:
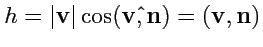
. Тогда,
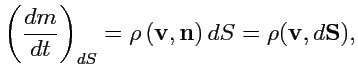 |
(85) |
где
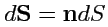
- ориентированный элемент поверхности. Полное количество жидкости,
протекающей через всю поверхность

, будет определяться интегралом
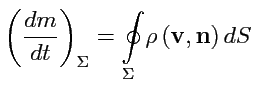 |
(86) |
и называется
потоком жидкости через поверхность 
.
Рассмотрим общее определение потока векторного поля. Пусть в некоторой области пространства задано
векторное поле
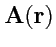
и поверхность

. Тогда:
потоком поля
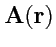 через поверхность
через поверхность  называется величина
называется величина
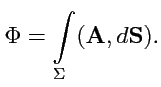 |
(87) |
Особый интерес для исследования векторных полей представляет поток через замкнутую поверхность:
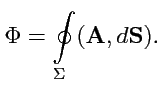 |
(88) |
Рассмотрим более подробно эту величину также на гидромеханическом примере. Поместим в поток
жидкости замкнутую поверхность
a

Рис.26 К определению потока векторного поля.

(рис.
26). Тогда, по смыслу выражения (
86),
если жидкость однородна, то количество жидкости, "втекающей" внутрь

, будет очевидно
равно количеству вытекающей и в этом случае
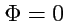
. Ситуация изменится, если внутрь

поместить кусочек тающего льда. Тогда, за счет "производства" жидкости внутри

вытекать
будет больше, чем "втекать" и, следовательно, в этом случае
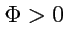
. Аналогично, если внутри

жидкость будет каким-либо образом поглощаться, то

. В первом случае
(
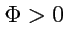
) говорят, что внутри
 есть источник
есть источник, во втором (

) -
сток;
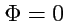
-
источников или стоков поля нет. Эти определения можно распространить для
произвольного поля
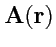
Таким образом, величину потока векторного поля через замкнутую поверхность можно рассматривать
как характеристику самого поля. Тогда, векторное поле можно исследовать, помещая пробную
замкнутую поверхность в различные области поля и определяя поток
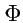
. Если разделить
величину потока
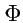
на объем
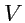
, захваченный поверхностью

, то можно получить в
области поля среднюю
плотность потока или среднюю
мощность источника поля (если
он есть внутри). Однако из-за конечных размеров пробной поверхности результаты таких
исследований могут оказаться неоднозначными, например, если внутри окажутся два одинаковых по мощности
источник и сток. Выбор поверхности также выглядит неоднозначно. Чтобы избавиться от такой
зависимости и неоднозначности, будем, как и при рассмотрении градиента скалярного поля,
стягивать поверхность к некоторой точке

. Тогда, в пределе
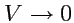
,

, если он существует, будет получена величина мощности источника поля
в точке

. Эта величина называется
дивергенцией векторного поля и обозначается как
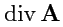
(от
divergentia - расходимость). Согласно такому определению, дивергенция
векторного поля
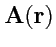
вычисляется как
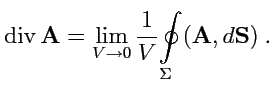 |
(89) |
Выражение (
89) определяет характеристику поля
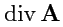
инвариантным способом.
Выберем в области задания поля
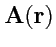
декартову систему координат. Тогда
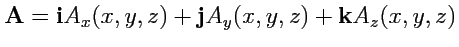
. Вычислим поток поля
через замкнутую поверхность

:
![$\displaystyle \displaystyle{\oint\limits_{\Sigma}} ({\mathbf A},{\mathbf n})dS ...
...imits_{\Sigma}} \left[ A_x\cos\alpha + A_y\cos\beta + A_z\cos\gamma \right] dS.$](img571.png) |
(90) |
Применяя теорему о среднем к правой части (
90)
![\begin{displaymath}\begin{array}{cc} \displaystyle{\oint\limits_{\Sigma}} ({\mat...
...ystyle{\frac{\partial A_z}{\partial z}} \right]_M V \end{array}\end{displaymath}](img572.png) |
(91) |
и переходя к пределу
из (
91), получим
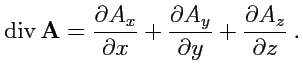 |
(92) |
Выражение (
92) является формулой для вычисления дивергенции поля
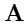
в декартовой системе координат. Из определения (
89) и (
92) следует, что
дивергенция
векторного поля,
 , является скалярной величиной
, является скалярной величиной, точнее скалярным полем.
Перечислим свойства дивергенции:
1. |
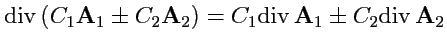 |
(93) |
1. |
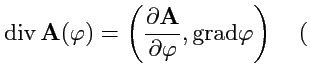 сложное поле сложное поле |
(94) |
Пример 3-9. Дано векторное поле

. Вычислить

Решение. Используем формулу (92), тогда
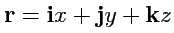
и
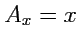
,
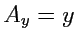
,
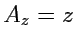
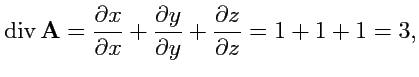 т. е.
т. е.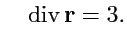
Пример 3-10. Вычислить дивергенцию напряженности электрического поля точечного заряда
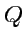
.
Решение.Напряженность поля точечного заряда
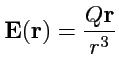
, где
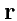
- радиус-вектор с началом в точке расположения заряда
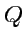
.
Так как
то
Таким образом, если
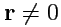
, то
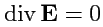
. В точке

дивергенция
неопределена (
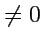
!). Несмотря на такую особенность можно вычислить поток
поля
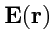
через поверхность, окружащую заряд
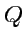
. Выберем в качестве такой
поверхности

сферу радиуса
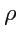
с центром в начале координат, где расположен и
сам заряд. На поверхности сферы модуль напряженности поля
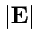
будет постоянным, а направление векторов поля (по радиусу) совпадает с направлением нормали

к этой поверхности. Поэтому
Полученный результат, в соответствии с условием задачи можно интерпретировать следующим
образом: в пространстве, окружающем заряд, источников электрического поля нет, так как
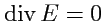
, но в начале координат источник есть, так как

и поток
поля через замкнутую поверхность также отличен от нуля. На этом основании естественно
будет считать, что заряд и есть источник электрического поля. (Результат

в электростатике носит название теоремы Гаусса).
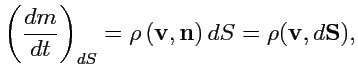
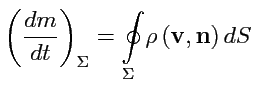
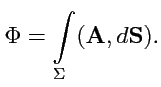

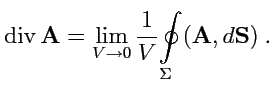
![$\displaystyle \displaystyle{\oint\limits_{\Sigma}} ({\mathbf A},{\mathbf n})dS ...
...imits_{\Sigma}} \left[ A_x\cos\alpha + A_y\cos\beta + A_z\cos\gamma \right] dS.$](img571.png)
![\begin{displaymath}\begin{array}{cc} \displaystyle{\oint\limits_{\Sigma}} ({\mat...
...ystyle{\frac{\partial A_z}{\partial z}} \right]_M V \end{array}\end{displaymath}](img572.png)
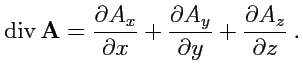
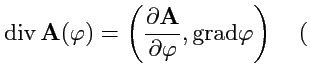 сложное поле
сложное поле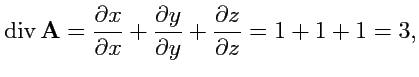 т. е.
т. е.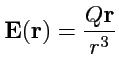 , где
, где