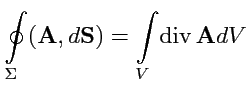Теорема Остроградского-Гаусса для векторных полей

3. Дифференциальные характеристики полей

3.4. Теорема Оcтроградского-Гаусса для векторных полей.

С использованием выражениния (92) для дивергенции векторного поля, формула ( 91) может быть переписана:

$\displaystyle \displaystyle{\oint\limits_{\Sigma}} ({\mathbf A},d{\mathbf S}) = \displaystyle{\int\limits_V} {\rm div}\,{{\mathbf A}} dV$

(95)

и в таком виде выражает содержание теоремы Остроградского-Гаусса для векторных полей:

- если компоненты векторного поля непрерывны на поверхности и в объеме, который она охватывает, то поток векторного поля равен интегралу от дивергенции по объему.


			Содержание