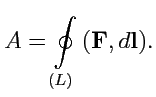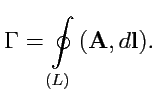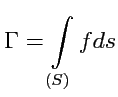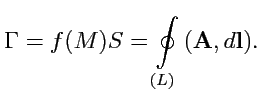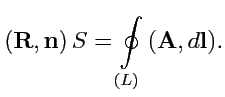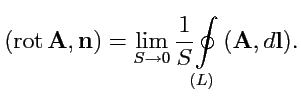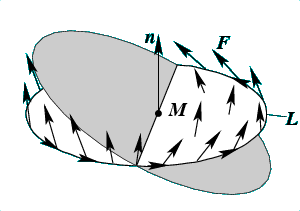
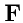
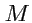
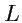
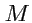
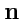
Пусть в некоторой области пространства задано силовое векторное поле . Выберем в этом поле площадку и точку на ее поверхности. Пусть эта площадка ограничена контуром . Построим в точке нормаль к плошадке по правилу "правого винта". Так как силовое поле задано во всем пространстве, то оно также

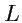
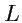
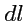
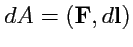
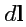
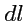
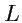
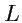
задано и в каждой точке на контуре . Вычислим работу, которая совершается при обходе контура . Работа на участке контура , где вектор по величине равен и направлен по касательной в контуру . Полная работа при обходе контура (рис. 28):

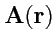
Аналогичная величина, определенная для произвольного векторного поля называется циркуляцией векторного поля 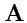по контуру :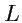

В рассмотренном примере работа (96) есть циркуляция силового поля.

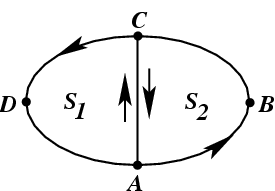
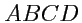
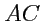
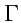
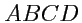
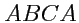
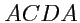
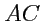
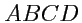
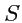
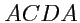
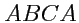
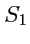
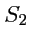
      Рассмотрим свойства циркуляции (97). Разделим замкрутый контур (рис. 29) на две части отрезком . Тогда, цикруляция по всему контуру будет равна сумме циркуляций по контурам и , так как по отрезку проход осуществляется дважды в противоположных направлениях. Пусть контур охватывает площадь , а контуры и соответственно и . Тогда, можно записать:

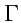
Из (98) следует, что можно представить в виде интеграла по поверхности, опирающейся на контур :

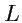
и, используя теорему о среднем, (99) далее можно записать как:

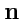
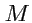
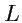
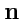
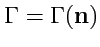
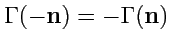
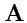
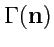
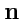
Будем изменять ориентацию вектора (рис. 28), сохраняя его начало в точке . Так как контур будет изменять свою ориентацию в поле, то величина циркуляции также будет изменяться и ее можно рассматривать как функцию : . При этом , так как направление обхода в этом случае будут противоположным. Так как поле считается непрерывным, то будет непрерывной функцией . Из анализа известно, что если непрерывная функция на ограниченном участке меняет свой знак, то она проходит через 0. 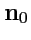Поэтому существует такой вектор , что . 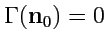Частный случай такой ситуации возникает на примере с силовым полем, когда векторы поля будут перпендикулярны к площадке, охватываемой контуром . 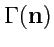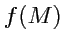Функцию , удовлетворяющую перечисленным свойствам, можно построить, если выбрать в виде

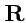
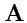
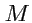
при этом вектор должен быть связан с самим полем в точке . Таким образом, можно записать

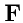
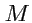
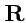
Из (102) в применении к силовому полю следует, что если в окрестности точки вектор отличен от нуля, то поле будет совершать работу при перемещении материальной точки по замкнутому контуру и наоборот.

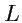
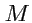
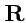
      Будем стягивать контур к точке . Тогда, в предельном случае формулы (102) вектор называется ротором векторного поля :

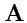
Формула (103) инвариантным образом определяет новую характеристику векторного поля - ротор, который векторным полем.