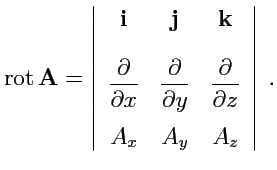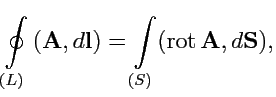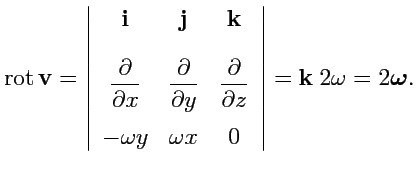3. Дифференциальные характеристики полей

Теорема Остроградского-Гаусса для векторных полей 3.6. Теорема Стокса для векторных полей. Вычисление ротора поля в декартовой системе координат. Физический смысл ротора Оператор Гамильтона ...


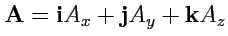
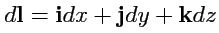
Пусть $ {\mathbf A}={\mathbf i}A_x+{\mathbf j}A_y+{\mathbf k}A_z$, тогда, так как $ d{\mathbf l}={\mathbf i}dx+{\mathbf j}dy+{\mathbf k}dz$, то, используя теорму Стокса
\begin{displaymath}\begin{array}{l} \displaystyle{\oint\limits_{(L)} \left({{\ma... ...ial A_x}{\partial y}} \right]\cos\gamma \biggr\}\ . \end{array}\end{displaymath} (104)
Применяя теорему о среднем к (104) и переходя к пределу (97),
$\displaystyle {\rm rot}\,{\mathbf A} = {\mathbf i}\left[ \displaystyle{\frac{\p... ...rtial A_y}{\partial x}}-\displaystyle{\frac{\partial A_x}{\partial y}} \right].$ (105)
Формула (105) определяет способ вычисления ротора поля в декартовой системе координат. На основе известных свойств определителей это выражение можно переписать также в виде:
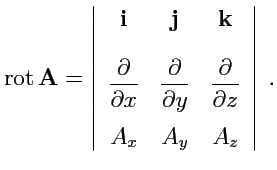(106)
С использованием (105), (104) можно переписать в виде:
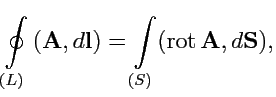$\displaystyle \displaystyle{\oint\limits_{(L)} \left({{\mathbf A}},{d{\mathbf l... ...ht) } = \displaystyle{\int\limits_{(S)}} ({\rm rot}\,{\mathbf A},d{\mathbf S}),$ (107)
что выражает содержание теоремы Стокса для векторных полей:
      - циркуляция векторного поля по замкнутому контуру 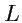$ L$ равна потоку ротора поля через поверхность, которая опирается на этот контур.

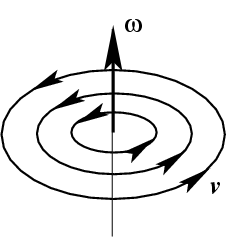
Рис.29 Поле скоростей

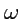
      Пример 3-11. Вычислить ротор векторного поля скоростей точек твердого тела, вращающегося вокруг своей оси с угловой скоростью $ \omega$.

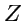
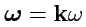
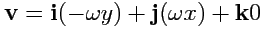
      Решение. Пусть ось вращения направлена по оси $ Z$. Из механики известно, что скорость $ {\mathbf v}=[{\boldsymbol \omega},{\mathbf r}]$, где вектор угловой скорости $ {\boldsymbol \omega}={\mathbf k}\omega$. Отсюда, $ {\mathbf v}={\mathbf i}(-\omega y)+{\mathbf j}(\omega x) + {\mathbf k} 0$ и тогда

$\displaystyle {\rm rot}\,{\mathbf v} = \left\vert \begin{array}{ccc} {\mathbf i... ...& 0 \\ \end{array}\right\vert = {\mathbf k}\;2\omega = 2{\boldsymbol \omega}. $
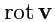
С помощью этого примера можно выяснить физический смысл ротора векторного поля. Ротор поля скоростей, $ {\rm rot}\,{\mathbf v}$, как видно, совпадает по направлению с вектором угловой скорости. Таким образом, ротор поля во многих случаях условно можно считать "осью", вокруг которой, по правилу правого винта, "закручены" векторные линии этого поля, (рис. 29). Отсюда происходит и термин rotor - вихрь.
     Векторное поле, для которого ротор отличен о нуля, называется вихревым. При этом, векторные линии этого поля замкнуты (или замыкаются на бесконечности), а ротор направлен перпендикулярно векторной линии, так, что если смотреть из конца положительного направления ротора, то векторная линия должна быть направлена против часовой стрелки.
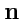
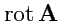
     Формула (103) может оказаться не совсем удобной, так как несмотря на то, что она определяет ротор, но вычислить позволяет лишь его проекцию на некоторе направление $ {\mathbf n}$. Поэтому, имеет смысл преобразовать это это выражение так, чтобы получить непосредственно вектор $ {\rm rot}\,{\mathbf A}$.
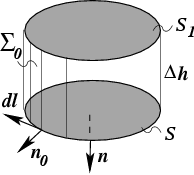
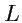
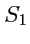
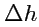
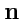
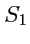
     Рассмотрим контур $ L$, охватывающий площадку $ S_1$. Построим на этой площадке цилиндр с образующей высоты $ \Delta h$, направленной вдоль нормали $ {\mathbf n}$ к $ S_1$ (рис. 30). Проинтегрируем обе части определения (103) вдоль образующей цилиндра:

Рис.30 К вычислению ротора векторного поля
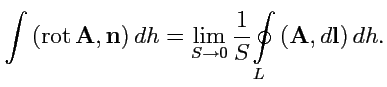$\displaystyle \int \left({{\rm rot}\,{{\mathbf A}}},{{\mathbf n}}\right) dh = \... ...{S}}\displaystyle{\oint\limits_{L}}\left({{\mathbf A}},{d{\mathbf l}}\right)dh.$ (108)
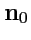
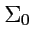
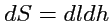
Если $ {\mathbf n}_0$ - нормаль к боковой поверхности цилиндра, то $ d{\mathbf l}=\left[{{\mathbf n}},{{\mathbf n}_0}\right]dl$ и $ \left({{\mathbf A}},{d{\mathbf l}}\right) = ({\mathbf A},[{\mathbf n},{\mathbf n}_0])dl$. Тогда правая часть (108) запишется как интерал по боковой поверхности цилиндра $ \Sigma_0$ ($ dS=dldh$):
$\displaystyle \int\displaystyle{\oint\limits_{L}}\left({{\mathbf A}},{d{\mathbf... ...ht)dh = \int\limits_{(\Sigma_0)}{} ({\mathbf n},[{\mathbf n}_0,{\mathbf A}])dS.$ (109)
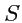
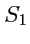
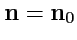
Последний интеграл преобразуется к интегралу по всей поверхности цилиндра, если учесть, что интегралы типа (109), вычисленные на основаниях $ S$ и $ S_1$, равны нулю, так как здесь $ {\mathbf n}={\mathbf n}_0$, поэтому:
$\displaystyle \int \left({{\rm rot}\,{{\mathbf A}}},{{\mathbf n}}\right) dh = \... ...splaystyle{\oint\limits_{(\Sigma)}}({\mathbf n},[{\mathbf n}_0,{\mathbf A}])dS.$ (110)
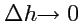
Применяя теорему о среднем к левой части (110) и устремляя$ \Delta h\hspace{-0.3em}\rightarrow 0$, получим:
$\displaystyle ({\rm rot}\,{{\mathbf A}},{\mathbf n})_M = \lim_{S\to 0,\Delta h\... ...splaystyle{\oint\limits_{(\Sigma)}}({\mathbf n},[{\mathbf n}_0,{\mathbf A}])dS.$ (111)
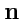
Так как вектор $ {\mathbf n}$ в левой части (111) в отношении интегрирования является константой, то окончательно получаем:
$\displaystyle {\rm rot}\,{{\mathbf A}}=\lim_{V\to 0} \displaystyle{\frac{1}{V}} \oint [{\mathbf n}_0,{\mathbf A}]dS.$ (112)
Выражение (112) является эквивалентным (103) и также может рассматриваться, как определение ротора векторного поля.

Скалярные и векторные поля Векторный анализ в криволинейных координатах
Циркуляция векторного поля. Ротор   Содержание   Оператор Гамильтона ...