3. Дифференциальные характеристики полей
 3.2. Градиент скалярного поля. Производная по направлению
3.2. Градиент скалярного поля. Производная по направлению 
Пусть в некоторой области 3-х мерного пространства задано скалярное поле

.
Выберем в этой области точку

. Если перемещаться из этой точки вдоль какой-либо линии,
то поле будет меняться от точки к точке. Причем, ясно, что для различных направлений скорость
изменения
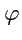
также может оказаться различной и должна характеризовать само поле в
рассматриваемой точке или ее окрестности. При этом, по смыслу рассуждений, эта величина
должна быть векторной. Рассмотрим строгое определение этой характеристики на примере
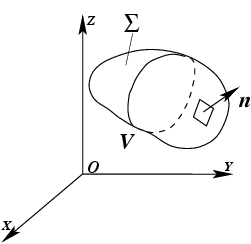
гидромеханической аналогии. Пусть в пространстве задано скалярное поле давления жидкости
или газа. Поместим в эту область тело произвольной формы, ограниченное поверхностью

,
(рис.
24). Вычислим суммарую силу
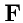
, действующую на тело со стороны среды.
Рис.24 К определению градиента скалярной функции
Рассмотрим площадку
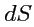
, содержащую точку

на поверхности

. Модуль силы, действующей
на площадку
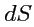
, равен
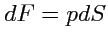
, а направление совпадает с направлением нормали к поверхности
в точке

. Таким образом, вектор силы
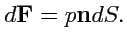 |
(71) |
Полная сила может быть вычислена интегрированием по поверхности

:
 |
(72) |
Если результат (
72) разделить на объем
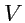
, заключенный внутри поверхности

,
то получившаяся величина
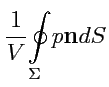 |
(73) |
будет "средней" силой, действующей со стороны среды на любую точку внутри

. Физической
причиной этого действия является перепад давлений между различными точками среды.
Способность поля (в данном случае поля давлений) оказывать действие на пробное тело является
характеристикой самого поля и поэтому не должна зависеть на формы и размеров тела, помещенного
в это поле. Будем стягивать поверхность

к точке

, устремляя, таким образом,
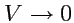
и рассмотрим предел
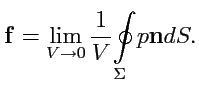 |
(74) |
Если предел (
74) существует, то по смыслу рассуждений он определит плотность
силы, действующей со стороны поля (давлений) на точечное тело, помещенное в точку

и
будет характеризовать быстроту изменения поля (перепад давлений) в окрестности этой точки.
Рассмотрим общий случай скалярного поля

. Если для поля

существует предел (
74) при стягивании поверхности к точке

, то он называется
градиентом поля

в этой точке:
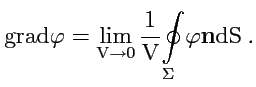 |
(75) |
По определению
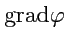
является вектором и вообще, выражение (
75),
будучи примененным в каждой точке области определения поля
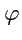
, будет задавать
векторное поле градиента
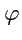
.
Формула (
75) задает определение
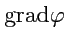
в форме, независящей от
системы координат - инвариантно. Пользуясь (
75), получим формулу вычисления
градиента скалярного поля в декартовой системе координат. Тогда, так как вектор нормали

:
![$\displaystyle \displaystyle{\oint\limits_{\Sigma}} \varphi{\mathbf n}dS = \disp...
... + {\mathbf j}\varphi\cos(\beta) + {\mathbf k}\varphi\cos(\gamma) \right] dS\ .$](img527.png) |
(76) |
Применим к каждому слагаемому (
76) формулу Остроградского-Гаусса (3.1):
![$\displaystyle \displaystyle{\oint\limits_{\Sigma}} \varphi{\mathbf n}dS = \disp...
... y}} + {\mathbf k}\displaystyle{\frac{\partial \varphi}{\partial z}} \right]dV.$](img528.png) |
(77) |
Применяя теорему о среднем к правой части (
77), получим
![$\displaystyle \displaystyle{\oint\limits_{\Sigma}} \varphi{\mathbf n}dS = \left...
... + {\mathbf k}\displaystyle{\frac{\partial \varphi}{\partial z}} \right]_M V\ ,$](img529.png) |
(78) |
переходя к пределу
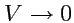
и сравнивая с определением градиента (
75), получим
формулу для вычисления градиента в декартовой системе координат:
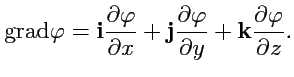 |
(79) |
Производная по направлению. Выберем в пространстве, где задано скалярное поле

некоторое направление с помощью единичного вектора
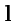
. Считая,
что этот вектор определяет координатную ось
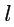
и пользуясь правилом дифференцирования
сложной функции, вычислим производную
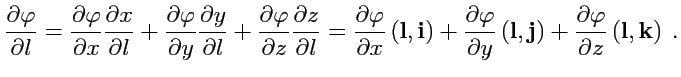 |
(80) |
Полученное выражение, учитывая, что
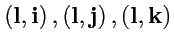
-
координаты вектора
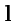
,можно переписать как скалярное произведение
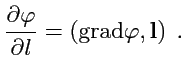 |
(81) |
Это выражение (
81) называется
производной по направлению
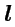 поля
поля 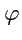
.
Формула (
79) позволяет получить следующие свойства и правила вычисления
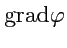
:
Пример 3-8. Вычислить градиент поля

, где
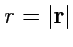
- модуль
радиус-вектора,
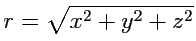
.
Решение. Согласно выражению (
79), получим
Аналогично,
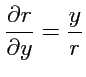
,
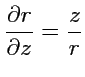
и тогда, складывая
вычисленные производные, получим:
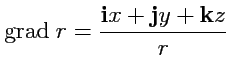
или в бескоординатной форме

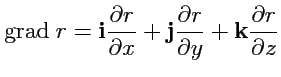

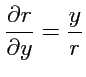 ,
,
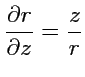 и тогда, складывая
вычисленные производные, получим:
и тогда, складывая
вычисленные производные, получим:
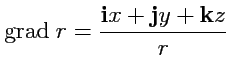 или в бескоординатной форме
или в бескоординатной форме