Интегральные теоремы

Ранее при определении полей и рассмотрении их общих характеристик указывалось на связь полей (скалярных, векторных) с функциями нескольких переменных. Поэтому в анализе полей, т. е. исследовании дифференциальных (в точке) и интегральных (в области) характеристик полей важную роль играют теоремы из анализа функций. Сформулируем без доказательства две основные теоремы, которые будут часто применяться в дальнейшем.

- если функции , , непрерывны вместе со своими частными производными внутри объема и на поверхности $\Sigma$ , то имеет место формула:

$\begin{displaymath}\begin{array}{l} \displaystyle{\int\limits_{V}} \left[ \displ... ...pha) + A_2\cos(\beta) + A_3\cos(\gamma) \right] dS, \end{array}\end{displaymath}$

(68)

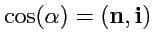
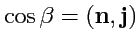
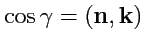
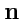
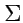
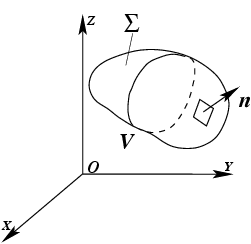
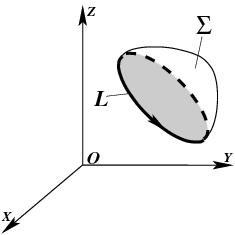
где $\cos(\alpha)=\left({\mathbf n},{\mathbf i}\right)$ , $\cos{\beta}=\left({\mathbf n},{\mathbf j}\right)$ , $\cos{\gamma}=\left({\mathbf n},{\mathbf k}\right)$ - направляющие косинусы вектора нормали ${\mathbf n}$ к поверхности $\Sigma$ (рис. 22).

В качестве комментария к формуле Остроградского-Гаусса можно отметить, что ее можно рассматривать как обобщение формулы Ньютона-Лейбница

которая сводит вычисление интеграла от производной к значениям самой функции на границах интервала интегрирования (интеграл по поверхности в формуле (68)).

если функции , , непрерывны вместе со своими частными производными на поверхности $\Sigma$ , опирающейся на контур (рис. 23), то имеет место формула:

$\begin{displaymath}\begin{array}{l} \displaystyle{\oint\limits_{\Sigma}} \left\{... ...tyle{\oint\limits_{L} } A_1 dx + A_2 dy + A_3 dz\ . \end{array}\end{displaymath}$

(70)