2. Скалярные и векторные поля
 2.7 Задачи для самостоятельной работы
2.7 Задачи для самостоятельной работы 
I. Найти поверхности уровня скалярных полей:
1.
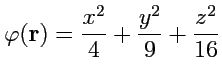
;
2.
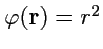
;
3.
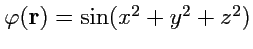
;
4.
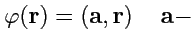
постоянный вектор;
5.
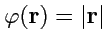
;
II. Построить линии уровня скалярных полей:
1.
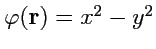
;
2.
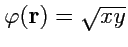
;
3.
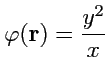
;
4.
![$ \varphi({\mathbf r}) = \rm {exp}\left[ \displaystyle{\frac{2x}{x^2+y^2}}\right]$](img493.png)
;
III. Найти векторные линии полей в пространстве и на плоскости:
1.
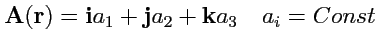
;
2.
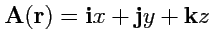
;
3.
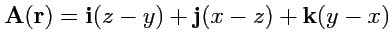
;
4.
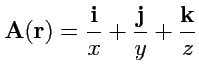
;
5.
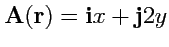
;
6.
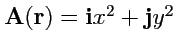
;
7.
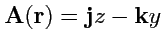
;
8.
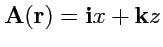
;
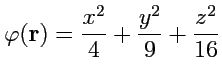 ;
;
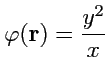 ;
;
![$ \varphi({\mathbf r}) = \rm {exp}\left[ \displaystyle{\frac{2x}{x^2+y^2}}\right]$](img493.png) ;
;
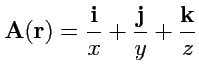 ;
;