2. Скалярные и векторные поля
 2.6 Векторное поле. Векторные линии
2.6 Векторное поле. Векторные линии 
Определение поля можно распространить и на векторные величины. Тогда:
-
если в каждой точке пространства М, принадлежащей некоторой области трехмерного
пространства задать вектор
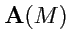 , то таким образом будет задано векторное поле.
, то таким образом будет задано векторное поле.Вектор
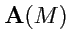
(рис.
16) называется вектором поля.
Рис.16. К определению векторного поля.
Примером векторного поля является поле сил тяготения, возникающее в пространстве вокруг
материального тела. При этом на пробное тело будет действовать сила, величина и направление
которой будет зависеть от положения этого пробного тела в пространстве.
При произвольном течении жидкости скорости частиц в общем случае также будут зависеть от
их пространственного положения, образуя, следовательно, векторное
поле. Векторное поле является векторной функцией векторного аргумента.
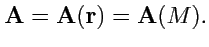 |
(62) |
Если в области определения векторного поля ввести декартову систему координат, то вектор поля
можно разложить по ортам
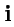
,
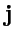
,
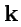
:
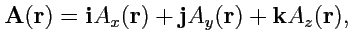 |
(63) |
при этом
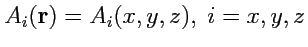
. Таким образом,
задание векторного поля
в системе координат означает задание трех независимых функций трех переменных.
Будем считать, что все функции
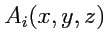
непрерывны и дифференцируемы, что обычно выполняется
в физических приложениях теории поля. Отдельные точки, где эти условия не выполнены (т. е. вектор
поля не определен или испытывает скачки), называются
особыми и требуют специального
рассмотрения.
Геометрической характеристкой векторного поля являются
векторные линии, т.е. кривые, в
любой точке которых касательная к ним совпадает с вектором поля
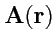
(
рис. 17).
Например, в случае стационарного течения жидкости векторные линии можно рассматривать как
траектории движения частиц жидкости, а количество линий будет пропорционально числу частиц.
Рис.17 К определению векторных линий.
Чтобы получить уравнение векторных линий, будем рассматривать сами линии как годограф некоторой
вектор-функции
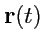
скалярного аргумента. Тогда вектор
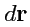
будет направлен по
касательной к векторной линии в точке с радиус-вектором
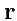
(
рис. 17). Следовательно, он
будет пропорционален вектору поля в этой точке:
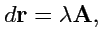 |
(64) |
где
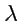
- некоторый коэффициент пропорциональности.В системе координат
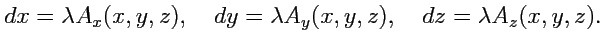 |
(65) |
Исключив из (
65)
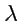
, получим систему
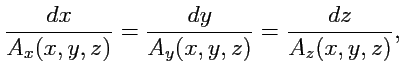 |
(66) |
которая называется системой дифференциалных уравнений векторных линий. Независимых
уравнений в этой системе только два и общее решение может быть представлено в виде:
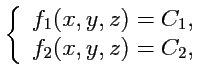 |
(67) |
и каждая векторная линия, таким образом, будет линией пересечения двух поверхностей
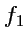
и
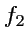
Пример 2-5. Построить векторные линии поля
![$ {\mathbf A}({\mathbf r})=\left[{\mathbf a},{\mathbf r}\right]$](img447.png)
, где

-
постоянный вектор, направленный вдоль оси
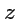
,
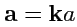
.
Решение. Согласно правилу вычисления векторного произведения в декартовой системе координат,
компоненты поля
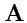
имеют вид:
и уравнение векторных линий (
66) принимает вид
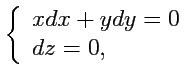
откуда
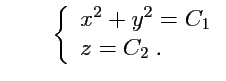
Полученная система определяет два семейства поверхностей: цилиндры с направляющей, параллельно
оси
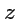
и плоскости, перпендикулярные оси
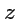
, следовательно, векторные линии поля
![$ {\mathbf A}({\mathbf r})=\left[{\mathbf a},{\mathbf r}\right]$](img447.png)
имеют вид окружностей, лежащих в плоскости
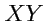
. Вид этого
семейства для значения
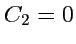
представлен на
рис. 2.8.
Рис.2.8. Векторные линии.
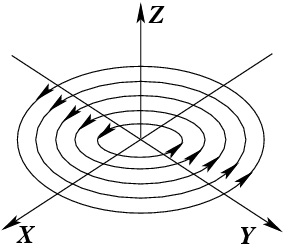
Пример 2-6. Построить силовые линии электрического плоского диполя с моментом
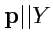
.
Решение. Напряженность поля плоского диполя имеет вид
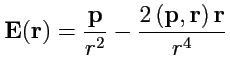
. Так как
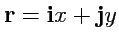
,
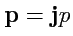
, то выражение для вектора поля в декартовой
можно записать как
и тогда уравнение векторных линий
После разделения переменных получим
Полученное уравнение после замены
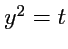
сводится к неоднородному уравнению Эйлера,
общее решение которого имеет вид
Для удобства построения преобразуем решение:
Таким образом, векторные линии поля
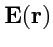
представляют собой семейство окружностей,
касающихся друг друга в начале координат (
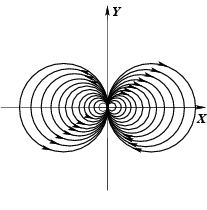
рис. 2.9). Если сравнить картину силовых линий поля
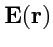
с линиями уровня скалярного поля
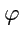
, рис. 2.5, то видно, что
рис. 2.9 отличается лишь поворотом на угол
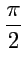
. В действительности далее будет показано,
что эти два поля связаны между собой.
Рис.2.9. Векторные линии поля плоского диполя.
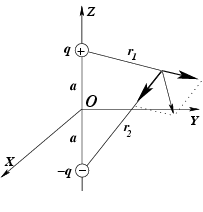
Пример 2-7. Построить силовые линии электрического поля системы из двух зарядов
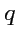
и
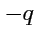
,
расстояние между которыми равно
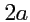
.
Решение. Поместим начало системы координат в середину отрезка, соединяющего заряды и лежащего на
оси
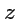
(
рис. 2.10). Так как система зарядов обладает осью симметрии, то картина силовых линий
будет одинаковой в любой плоскости, проходящей через ось
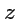
. Рассмотрим плоскость
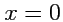
.
Напряженность поля точечного заряда определяется выражением
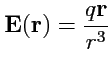
, где
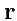
- радиус-вектор, проведенный из точки,
где расположен заряд, в точку наблюдения. Тогда, в настоящей задаче выражение для суммарного
поля двух зарядов запишется в виде
a
Тогда, уравнение векторных линий в плоскости
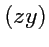
будет иметь вид:
В полученном уравнении можно разделить переменные, если ввести замену
Учитывая, что
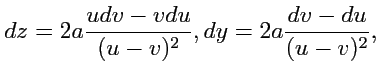
получим дифференциальное уравнение
После алгебраических преобразований
и интегрирования
Возвращаясь к переменным
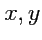
,
Полученное уравнение определяет семейство кривых (силовых линий) в плоскости
(рис. 2.11).
Рис.2.11. Силовые линия поля двух точечных зарядов.

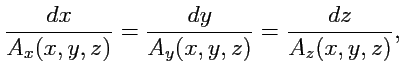
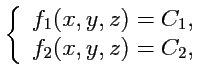
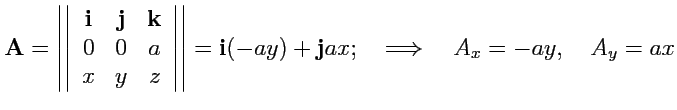
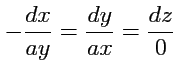
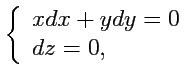 откуда
откуда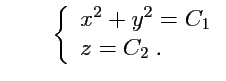
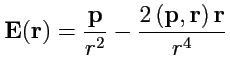 . Так как
. Так как
![\begin{displaymath}
\begin{array}{ccl}
{\mathbf E}({\mathbf r})& = & \displaysty...
...}{r^4}} \right] = {\mathbf i}E_x + {\mathbf j}E_y
\end{array}
\end{displaymath}](img459.png)
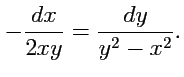
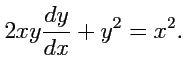
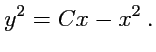
![$\displaystyle \left[ x+\displaystyle{\frac{1}{2}}C \right]^2 + y^2 = \left[\displaystyle{\frac{1}{2}}C \right]^2 .
$](img464.png)
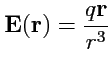 , где
, где
![$\displaystyle {\mathbf E}({\mathbf r})= \displaystyle{\frac{q{\mathbf r}_1}{r_1...
...left[
\displaystyle{\frac{y}{r_1^3}} - \displaystyle{\frac{y}{r_2^3}}
\right].
$](img473.png)
 a
a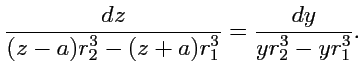

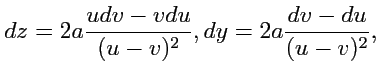 получим дифференциальное уравнение
получим дифференциальное уравнение
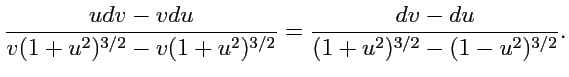
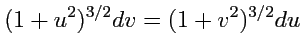
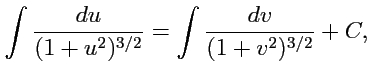
![$\displaystyle (z+a)[(z+a)^2+y^2]^{-1/2} - (z-a)[(z-a)^2+y^2]^{-1/2} = C
$](img485.png)