2. Скалярные и векторные поля
 2.5 Скалярное поле. Поверхности и линии уровня
2.5 Скалярное поле. Поверхности и линии уровня 
Рассмотрим в 3-х мерном пространстве некоторую область. Если в каждой точке
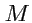
этой области
задать число (скаляр)
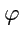
, то говорят, что задано
скалярное поле 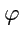
. Согласно
такому определению, скалярное поле является функцией точки. Так как положение точки
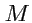
можно характеризовать ее радиус-вектором
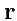
, то задание поля
будет означать, что установлено соответствие между
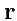
и
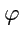
. Таким образом, поле можно
рассматривать как функцию векторного аргумента
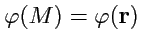
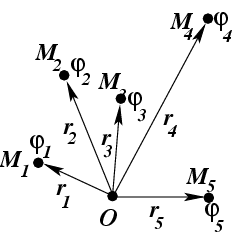
(рис.
13).
Рис.13. К определению скалярного поля
Если в области определения поля ввести декартову систему координат, то
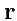
можно представить
как упорядоченную тройку чисел
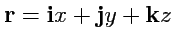
и тогда задание поля
будет эквивалентно заданию функции трех переменных
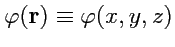
. В
дальнейшем будем считать эту функцию непрерывной и дифференцируемой.
Как известно, функцию одной переменной можно рассматривать как уравнение кривой на плоскости
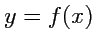
, двух переменных - как поверхность
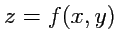
. Представить аналогичный "график" в случае поля
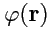
затруднительно, поэтому для наглядной характеристики поля
используют
поверхности уровня.
Поверхностью уровня поля
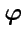 называют геометрическое место точек, в которых поле
принимает постоянное значение
называют геометрическое место точек, в которых поле
принимает постоянное значение. Согласно такому определению, уравнение поверхности уровня
будет иметь вид:
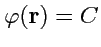 или или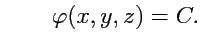 |
(61) |
Уравнение (
61) является уравнением поверхности, что объясняет соответствующее
название. Придавая
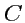
различные значения, можно получить наглядное представление о том, как
величина
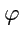
распределена в пространстве. При этом, если в некоторой области поле изменяется
быстро, поверхности уровня будут сближаться. Пересекаться они не могут, за исключением одной
точки.
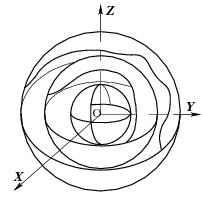
Рис.14. Поверхности уровня скалярного поля.
Пример 2-2. Рассмотрим поле вида
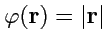
(или просто
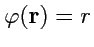
).
Уравнение (
61) принимает вид:
Так как
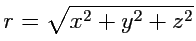
, то
и, таким образом, поверхностями уровня поля
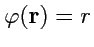
будет семейство концентрических
сфер с центром в начале координат (рис.
14).
Пример 2-3. Построить линии уровня плоского поля
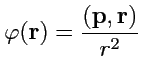
,
где
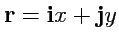
,
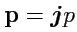
,
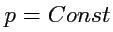
(2-х мерный аналог потенциала
электрического диполя).
Решение. Уравнение линий уровня имеет вид:
Рис.15. Линии уровня плоского поля.
Для различных значений
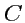
получается семейство окружностей с единственной общей точкой в начале
координат (рис.
15). В левой полуплоскости значения поля положительно, в правой - отрицательно,
а в точке
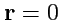
поле имеет особенность и неопределено.
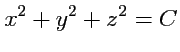
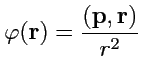 ,
где
,
где
![$\displaystyle py = C(x^2+y^2)\qquad \Longrightarrow\qquad
\left[ y-\displaystyle{\frac{1}{2}}Cp \right]^2 + y^2 = \left[ \displaystyle{\frac{1}{2}}C\right]^2.
$](img429.png)