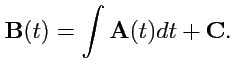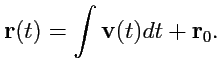2. Скалярные и векторные поля
 2.4 Интеграл от вектор-функции скалярного аргумента
2.4 Интеграл от вектор-функции скалярного аргумента 
Понятие производной вектор-функции позволяет дать определение неопределенного интеграла.
Пусть даны две вектор-функции
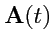
и
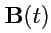
. Тогда
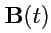
называется
неопределенным интегралом (первообразной)
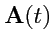
, если
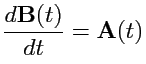
и обозначается как
В (
59) -
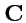
постоянный вектор (векторная константа) и это выражение
следует понимать как три независимых интеграла от функций
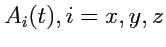
в какой-либо
системе координат, в частности, в декартовой. Например, в механике положение точки
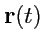
определяется, если известна ее скорость
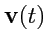
, как
Аналогично можно ввести понятие определенного интеграла от вектор-функции скалярного аргумента.
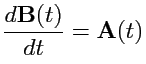 и обозначается как
и обозначается как