Использование сокращенной формы записи для векторного дифференцирования в координатной форме

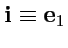
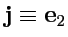
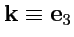
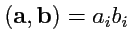
Наиболее просто основные операции векторного дифференцирования выглядят в декартовой системе координат. Будем считать, что ${\mathbf i}\equiv{\mathbf e}_1$ , ${\mathbf j}\equiv{\mathbf e}_2$ , ${\mathbf k}\equiv{\mathbf e}_3$ . Тогда, как известно, операции векторной алгебры могут быть записаны в виде: $({\mathbf a},{\mathbf b})=a_ib_i$ , $[{\mathbf a},{\mathbf b}]=\varepsilon_{ijk}{\mathbf e}_ia_jb_k$ и $({\mathbf a},[{\mathbf b},{\mathbf c}])=\varepsilon_{ijk}a_ib_jc_k$ , где

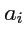
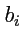
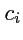
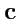
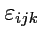
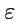
- координаты векторов ${\mathbf a}$ , ${\mathbf b}$ , ${\mathbf c}$ , $\varepsilon_{ijk}$ - $\varepsilon$ -символ (псевдотензор Леви-Чивиты), а по дважды повторяющимся индексам выполняется суммирование. С использованием таких обозначений:

1. $\displaystyle \quad$	$\displaystyle \nabla = {\mathbf e}_k\displaystyle{\frac{\partial }{\partial x_k}}$	(128)
2. $\displaystyle \quad$	$\displaystyle \nabla\phi = {\mathbf e}_k\displaystyle{\frac{\partial \phi}{\partial x_k}}$	(129)
3. $\displaystyle \quad$	$\displaystyle {\rm div}\,{\mathbf A} = (\nabla,{\mathbf A}) = \displaystyle{\frac{\partial A_k}{\partial x_k}} \phantom{aaaaaaaaaaaaaaaaaaaaaaa}$	(130)

4. $\displaystyle \quad$	$\displaystyle {\rm rot}\,{\mathbf A} = [\nabla,{\mathbf A}] = \varepsilon_{ijk}{\mathbf e}_i\displaystyle{\frac{\partial A_k}{\partial x_j}}$	(131)
5. $\displaystyle \quad$	$\displaystyle (\nabla\phi)_i = \displaystyle{\frac{\partial \phi}{\partial x_i}},$ следствие (129)	(132)
6. $\displaystyle \quad$	$\displaystyle ({\rm rot}\,{\mathbf A})_i = \varepsilon_{ijk}\displaystyle{\frac{\partial A_k}{\partial x_j}},$ следствие (131) $\displaystyle \hspace{30mm}$	(133)

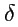
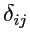
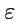
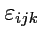
Использование (128)-(133) вместе в правилами обращения с $\delta$ -символом $\delta_{ij}$ и $\varepsilon$ -символом $\varepsilon_{ijk}$ также представляет удобный способ векторного дифференцирования. Для примера, докажем формулу (123):

$\begin{displaymath} \begin{array}{l} {\rm div}\,[{\mathbf A},{\mathbf B}] = \dis... ...thbf A}) - ({\mathbf A},{\rm rot}\,{\mathbf B}). \end{array} \end{displaymath}$

В последнем выражении, после дифференцирования, можно обратно вернуться к бескоординатной форме записи.


			Содержание