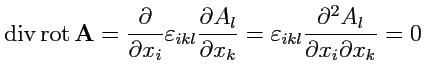Действие оператора

на скалярное или векторное поле порождает новые поля - векторные
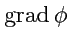
,
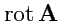
и скалярное поле
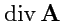
. К этим полям также можно применить
операции вычисления градиента, дивергенции и ротора. Всего, таким образом, можно построить
пять различных комбинаций
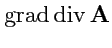
,
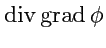
,
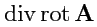
,
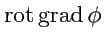
,
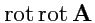
. Такие комбинации называются
дифференциальными
векторными операциями второго порядка. Рассмотрим более подробно наиболее важные из них.
1.
.
Оператор
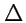
называется оператором Лапласа и (
134) дает его определение в
декартовой системе координат. С помощью оператора

оператор Лапласа можно записать
в бескоординатной, векторной форме:
Оператор Лапласа, в отличие от вектора

является скалярным оператором и поэтому может
применяться и к векторным, и к скалярным полям. Таким образом, выражение
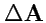
имеет смысл, так как умножение вектора на скаляр допустимо правилами векторной алгебры.
Тождества 2 и 3 выполяются для произвольных полей
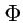
и
и очень часто используются
в практических приложениях векторного анализа.
.
Докажем тождество
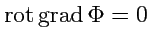
(
136) с помощью координатного способа
Так как
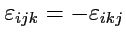
, а
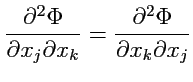
, то согласно известному тождеству
для свертки симметричного и антисимметричного тензора, получаем, что
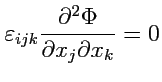
. Аналогично, для
(
137):
по тому же свойству свертки, что и выше.
![]() .
.
![]() .
.
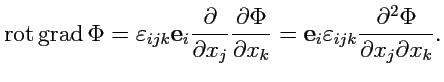
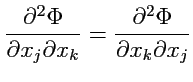 , то согласно известному тождеству
для свертки симметричного и антисимметричного тензора, получаем, что
, то согласно известному тождеству
для свертки симметричного и антисимметричного тензора, получаем, что
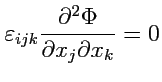 . Аналогично, для
(137):
. Аналогично, для
(137):