Специальные векторные поля

В физике большое значение играют векторные поля, для которых дивергенция, ротор или эти величины вместе, обращаются в ноль. Такие поля называются специальными. К ним относятся потенциальное, соленоидальное и Лапласово поля.

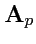
1. Потенциальное поле. Векторное поле ${\mathbf A}_p$ называется потенциальным, если в каждой его точке ротор поля равен нулю:

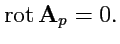$\displaystyle {\rm rot}\,{\mathbf A}_p = 0.$

(150)

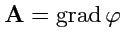
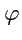
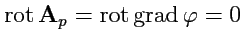
Согласно (150) и смыслу понятия ротор, потенциальное поле также называется безвихревым. Легко показать, что поле градиента, ${\mathbf A}={\rm grad}\,\varphi$ , где $\varphi$ - некоторое скалярное поле, является потенциальным. Действительно, согласно (135), ${\rm rot}\,{\mathbf A}_p={\rm rot}\,{\rm grad}\,\varphi=0$ . 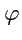Тогда потенциальное векторное поле ${\mathbf A}_p$ может быть представлено, как градиент скалярного поля $\varphi$ . 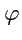Поле $\varphi$ называется потенциалом векторного поля

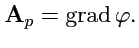$\displaystyle {\mathbf A}_p = {\rm grad}\,\varphi.$

(151)

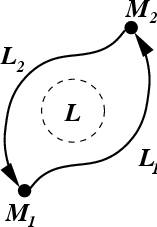
Потенциальное поле обладает одним важным свойством. Рассмотрим циркуляцию потенциального поля по замкнутому контуру (рис. 32). Применяя теорему Стокса для векторных полей (107), получим:

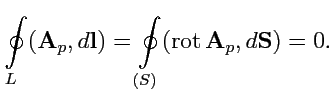$\displaystyle \oint\limits_{L}({\mathbf A}_p,d{\mathbf l}) = \oint\limits_{(S)}({\rm rot}\,{\mathbf A}_p,d{\mathbf S}) = 0.$

(152)

С другой стороны, если контур

в (152) состоит из двух частей

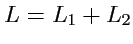
(рис. 32), то из (152) получаем:

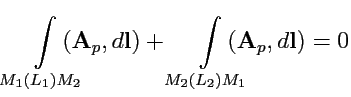$\displaystyle \int\limits_{M_1(L_1)M_2}\hspace{-1em} ({\mathbf A}_p,d{\mathbf l}) + \int\limits_{M_2(L_2)M_1}\hspace{-1em} ({\mathbf A}_p,d{\mathbf l}) = 0$

(153)

и следовательно

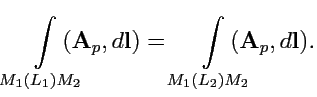$\displaystyle \int\limits_{M_1(L_1)M_2}\hspace{-1em} ({\mathbf A}_p,d{\mathbf l}) = \int\limits_{M_1(L_2)M_2} \hspace{-1em}({\mathbf A}_p,d{\mathbf l}).$

(154)

Рис.32 К вычислению циркуляции потенциального векторного поля

Равенство (154) означает, что циркуляция потенциального векторного поля между точкам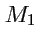и и 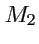не зависит от формы контура и следовательно определяется только их положением. С использованием (151) и определения производной по направлению (81) можно показать, что в (154)

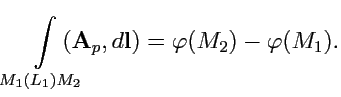$\displaystyle \int\limits_{M_1(L_1)M_2}\hspace{-1em} ({\mathbf A}_p,d{\mathbf l}) = \varphi(M_2) - \varphi(M_1).$

(155)

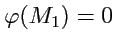
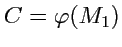
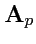
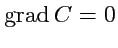
Полученное равенство может служить способом вычисления потенциала, если положить $\varphi(M_1)=0$ , что всегда можно сделать, добавив к полю $\varphi$ постоянное поле $C=\varphi(M_1)$ , которое не поменяет ${\mathbf A}_p$ , так как ${\rm grad}\,C=0$ .

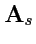
2. Соленоидальное поле. Векторное поле ${\mathbf A}_s$ называется соленоидальным, если в каждой его точке дивергенция обращается в ноль:

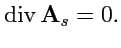$\displaystyle {\rm div}\,{\mathbf A}_s = 0.$

(156)

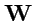
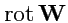
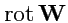
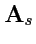
Рассмотрим векторное поле ${\mathbf W}$ и его ротор ${\rm rot}\,{\mathbf W}$ . Тогда из (137) для поля ${\rm rot}\,{\mathbf W}$ получим (156), т. е. соленоидальное поле ${\mathbf A}_s$ можно представить как ротор некоторого векторного поля:

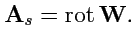$\displaystyle {\mathbf A}_s = {\rm rot}\,{\mathbf W}.$

(157)

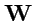
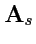
Поле ${\mathbf W}$ называется векторным потенциалом поля ${\mathbf A}_s$ .

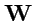
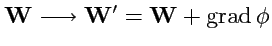
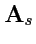
Отметим важную особенность векторного потенциала. Если ${\mathbf W}$ изменить, добавив к нему поле градиента ${\mathbf W}\longrightarrow {\mathbf W}'={\mathbf W}+{\rm grad}\,\phi$ , то поле ${\mathbf A}_s$ (157) при этом не изменится:

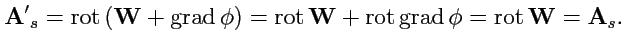$\displaystyle {\mathbf A'}_s = {\rm rot}\,({{\mathbf W}+{\rm grad}\,\phi}) = {\... ...{\mathbf W}+{\rm rot}\,{\rm grad}\,\phi = {\rm rot}\,{\mathbf W}={\mathbf A}_s.$

(158)

Таким образом, векторный потенциал определен неоднозначно.

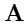
3. Лапласово (гармоническое) поле. Векторное поле ${\mathbf A}$ называется Лапласовым, если в каждой точке пространства для него одновременно выполняются условия:

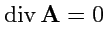$\displaystyle {\rm div}\,{\mathbf A}=0\$

(159)

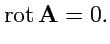$\displaystyle {\rm rot}\,{\mathbf A}=0.$

(160)

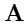
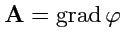
Так как (160) - это условие потенциальности поля, следовательно ${\mathbf A}$ можно представить как ${\mathbf A}={\rm grad}\,\varphi$ . Подставляя это выражение в (159), получим, учитывая (134), уравнение, определяющее поле $\phi$

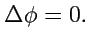$\displaystyle \Delta\phi = 0.$

(161)

Уравнение (161) называется уравнением Лапласа и, согласно (134), в декартовой системе координат оно имеет вид

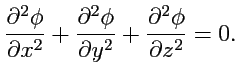$\displaystyle \displaystyle{\frac{\partial^2 \phi}{\partial x^2}}+\displaystyle... ...2 \phi}{\partial y^2}}+\displaystyle{\frac{\partial^2 \phi}{\partial z^2}} = 0.$

(162)

Функции, удовлетворяющие уравнению (162), называются гармоническими. Способы решения (162) и свойства гармонических функций рассматриваются в математический физике.


			Содержание