Чтобы выяснить смысл криволинейных координат, рассмотрим одно из уравнений (185) в виде:

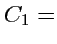
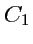
Const. Из аналитической геометрии известно, что это уравнение определяет в пространстве поверхность. Если изменяется, тогда, соответственно, будет задано семейство поверхностей. Аналогично можно получить еще два таких семейства:

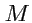
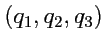
Если некоторая точка имеет криволинейные координаты , то из (188) - (190) следует, что она расположена на пересечении поверхностей (188) - (190) (рис. 34).

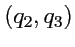
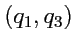
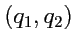
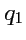
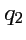
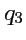
      Таким образом, положение точки в пространстве можно определить относительно семейства поверхностей (188)-(190), на каждой из которых соответствующая координата имеет постоянное значение. Поэтому, такие поверхности называются координатными. Попарные пересечения координатных поверхностей , , определяют пространственные кривые, вдоль которых изменяется только одна из координат, , или . Такие линии называются координатными линиями. Так как уравнения (188)-(190) в общем случае не обязательно задают плоскости, то и координатные линии также будут кривыми, что и определяет название криволинейная система координат.