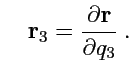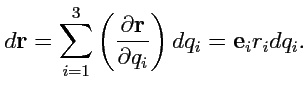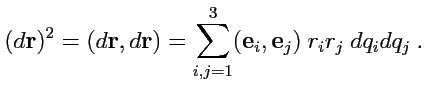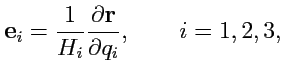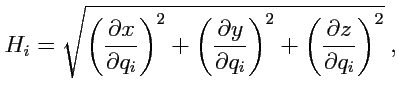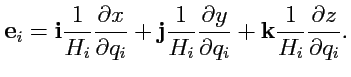4. Векторный анализ в криволинейных координатах
 4.3. Подвижный репер. Ортогональные криволинейные системы координат. Коэффициенты Ламэ
4.3. Подвижный репер. Ортогональные криволинейные системы координат. Коэффициенты Ламэ 
Как уже говорилось, положение точки
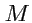
в пространстве можно определить относительно некоторой
точки отсчета с помощью кривоинейных координат:
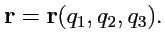 |
(191) |
При фиксированных
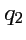
,
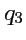
(
191) определяет уравнение координатной линии
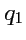
в
параметрической форме. Тогда, вектор
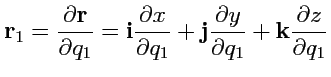 |
(192) |
будет направлен по касательной к этой координатной линии. Аналогично можно построить еще два
вектора, касательные к координатным линиям
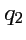
и
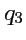
:
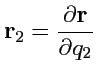 и и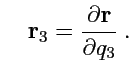 |
(193) |
Из условия (
186) следует, что смешанное произведение касательных векторов
![$\displaystyle ({\mathbf r}_1,[{\mathbf r}_2,{\mathbf r}_3]) \ne 0,$](img891.png) |
(194) |
что, как известно из векторной алгебры, означает, что тройка векторов
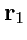
,
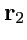
,
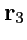
линейно независимы и, следовательно, образуют базис, по которому может быть
разложен (только в той точке, где этот базис построен !) произвольный вектор:
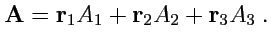 |
(195) |
Удобнее вместо векторов
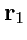
,
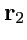
,
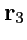
использовать единичные (нормированные)
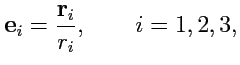 |
(196) |
где
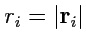
. Тройка векторов
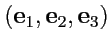
называется
репером
криволинейной системы координат.
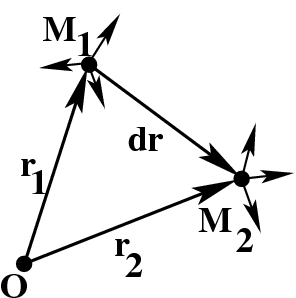
Рис.35 К определению подвижного репера
Базис декартовой системы координат, т. е. репер
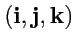
является одним из
простейших частных случаев общего определения. В общем случае ориентация векторов репера
(
196) может зависеть от положения точки, в которой он построен, согласно
(
192)-(
193). Поэтому репер криволинейной системы координат называют
локальным или подвижным репером. Это свойство определяет основное отличие криволинейных
систем координат от декартовой, в которой репер
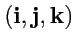
является одинаковым
во всех точках пространства.
Рассмотрим в пространстве две бесконечно близкие точки
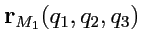
и
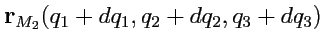
. Вектор
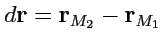
(рис.
35) может быть представлен в виде:
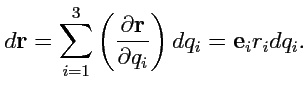 |
(197) |
Определим квадрат длины вектора
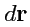
:
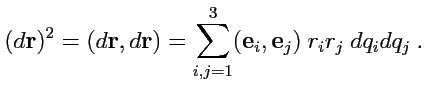 |
(198) |
Таким образом, в общем случае криволинейной системы координат квадрат длины представляет собой
квадратичную форму дифференциалов криволинейных координат, в отличие от теоремы Пифагора
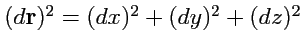
в декартовой.
Пусть выполняются условия:
Системы координат, для которых выполняются условия (
199), называются
криволинейными ортогональными. В дальнейшем будем ограничивать рассмотрение именно такими
системами. Тогда для векторов репера:
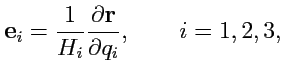 |
(200) |
где величины
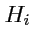
, определенные как
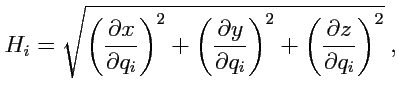 |
(201) |
называются
коэффициентами Ламэ. Так как
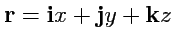
, то из
(
200) можно найти координаты векторов репера
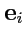
относительно декартовой
системы:
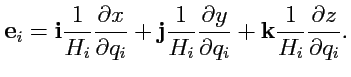 |
(202) |
Тогда квадрат длины и дифференциал вектора будут, выглядеть согласно
(
198)-(
199),
как
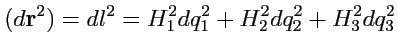 |
(203) |
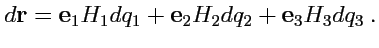 |
(204) |
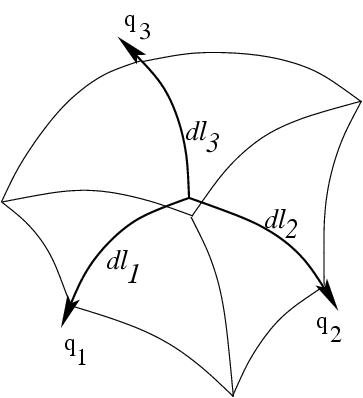
Рис.36 Бесконечно малый параллелепипед
Из (
204) следует, что величины
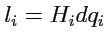
являются длинами ребер бесконечно малого
параллелепипеда (рис.
36). Отсюда получим выражение для элемента объема в криволинейной
системе координат:
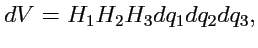 |
(205) |
известное из математического анализа.
![]() 4.3. Подвижный репер. Ортогональные криволинейные системы координат. Коэффициенты Ламэ
4.3. Подвижный репер. Ортогональные криволинейные системы координат. Коэффициенты Ламэ ![]()
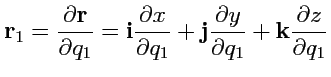
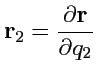 и
и