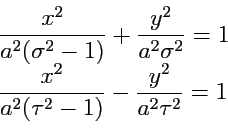4. Векторный анализ в криволинейных координатах
 4.4. Примеры координатных систем
4.4. Примеры координатных систем 
В этом разделе будут рассмотрены приложения общих положений, приведенных выше, на примерах наиболее распространенных
криволинейных систем координат.
1.
Декартова система является простейшей из всех систем. Положение точки определяется
тройкой чисел
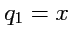
,
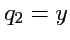
,
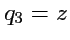
. Координатными поверхностями являются плоскости
Рис.37 Декартова система координат
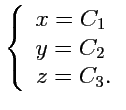 |
(206) |
Координатыми линиями являются прямые, параллельные осям
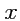
,
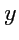
,
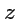
(рис.
37).
Коэффициенты Ламэ:
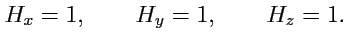 |
(207) |
Репер декартовой системы координат
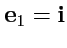
,
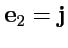
,
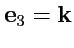
не
зависит от положения точки и векторы
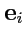
являются постоянными. Радиус-вектор любой точки
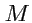
с координатами
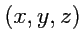
имеет вид:
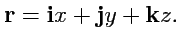 |
(208) |
Согласно (
205) и (
207) элемент объема имеет вид
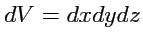
.
2.
Полярная система координат является примером криволинейной системы. В этой системе
(рис.
38):
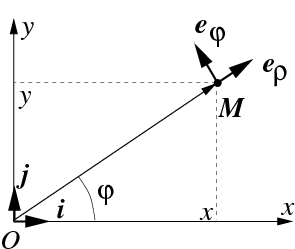
Рис.38 К определению полярной системы координат
Система (
184), согласно рис.
38, имеет вид:
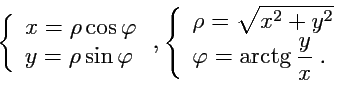 |
(209) |
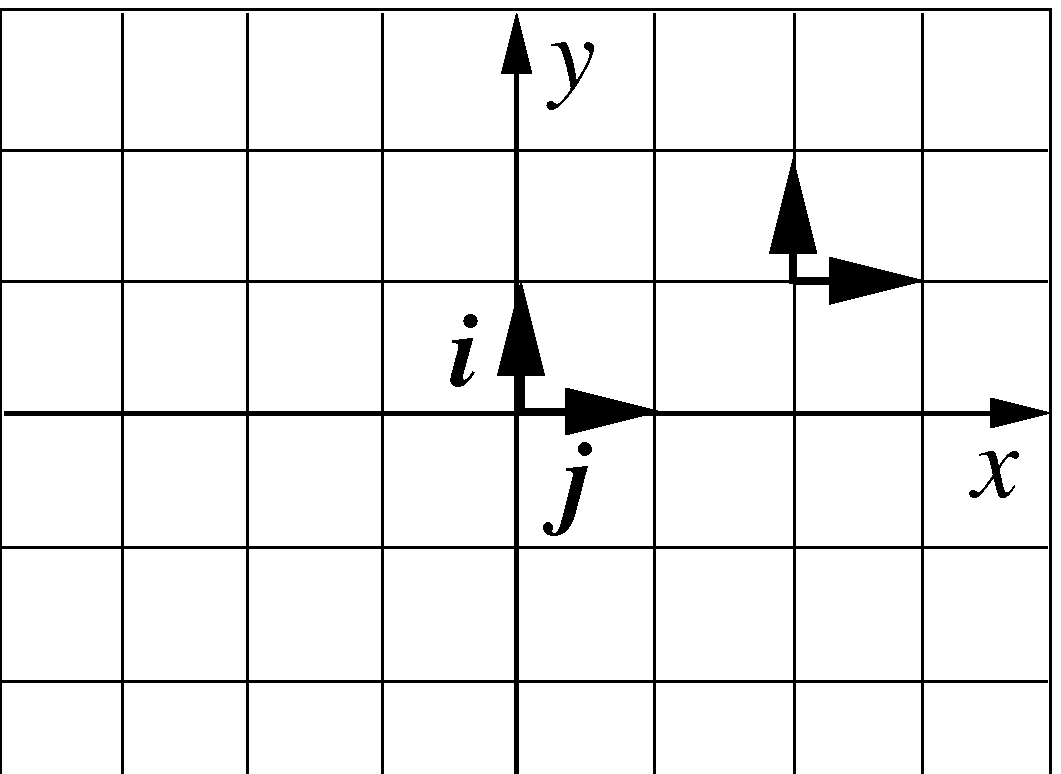
Рис.39 Полярная система координат
Тогда, координатные поверхности (в данном случае координатные линии) - окружности
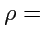
Const и прямые
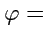
Const (рис.
39). Вычисляя коэффициенты
Ламэ по формулам (
201), получим:
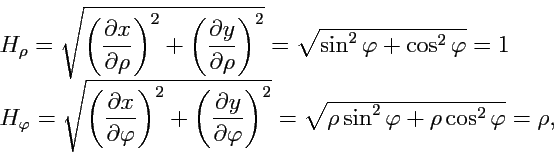 |
(210) |
откуда
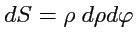
. Согласно (
202) векторы локального репера имеют
вид:
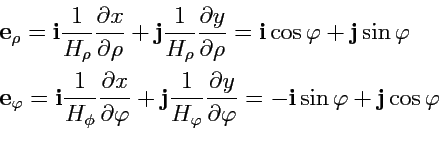 |
(211) |
и приведены на рис.
39. Используя (
211), можно записать радиус-вектор произвольной точки на плоскости в полярной системе координат как
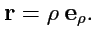 |
(212) |
3.
Цилиндрическая система координат представляет собой полярную систему, дополненную
осью
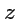
декартовой системы и задается соотношениями:
![$\displaystyle \hspace{-0.3em} \left\{\begin{array}{l} x = \rho\cos\varphi\\ [0....
...phi = \arctg\displaystyle{\frac{y}{x}}\\ [0.5em] z = z\\ \end{array}\ . \right.$](img941.png) |
(213) |
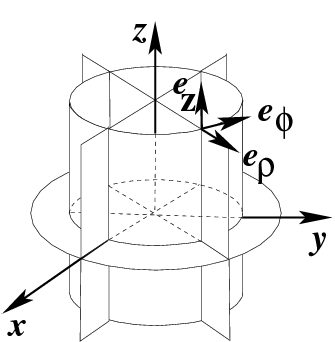
Рис.40 Цилиндрическая система координат
Согласно (
213), координатными поверхностями цилиндрической системы будут круговые
цилиндры (
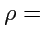
Const), плоскости, параллельные (
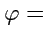
Const) и перпендикулярные
оси
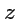
(
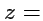
Const) (рис.
40). Коэффициенты Ламэ для цилиндрической системы:
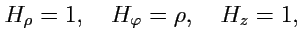 |
(214) |
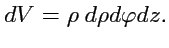 |
(215) |
Векторы локального базиса имеют вид:
![$\displaystyle \left\{\begin{array}{l} {\mathbf e}_\rho = {\mathbf i}\cos\varphi...
...athbf j}\cos\varphi\\ [0.5em] {\mathbf e}_z = {\mathbf k}\\ \end{array} \right.$](img945.png) |
(216) |
и радиус-вектор в цидиндрической системе координат запишется в виде
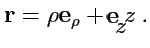 |
(217) |
4.
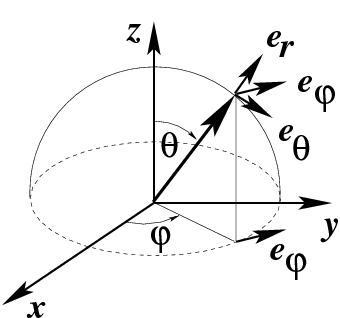
Сферическая система координат определяется координатами
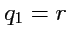
,
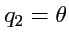
,
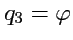
, где
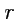
- модуль радиус-вектора
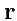
,
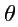
и
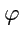
- соответственно
полярный и аксиальный углы (рис.
41), которые связаны с декартовыми координатами
соотношениями:
Рис.41 Сферическая система координат
![$\displaystyle \hspace{-9em} \left\{\begin{array}{l} x = r\sin\theta\cos\varphi\...
...em] y = r\sin\theta\sin\varphi\\ [0.5em] z = r\cos\theta.\\ \end{array} \right.$](img953.png) |
(218) |
Координатные поверхности - это концентрические сферы (
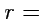
Const), конусы
(
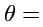
Const
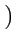
и плоскости, проходящие через ось
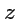
(
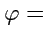
Const).
Пример сетки сферической системы координат дает система меридианов и параллелей на глобусе.
Коэффициенты Ламэ:
![$\displaystyle \left\{\begin{array}{l} H_r = 1\\ [0.5em] H_\theta = r\\ [0.5em] H_\varphi = r\sin\theta.\\ \end{array} \right.$](img957.png) |
(219) |
Элемент объема
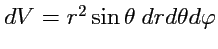
. Локальный базис
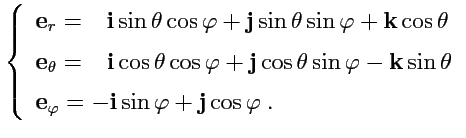 |
(220) |
Используя (
221), радиус-вектор в сферической системе координат можно записать в виде:
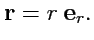 |
(221) |
5.
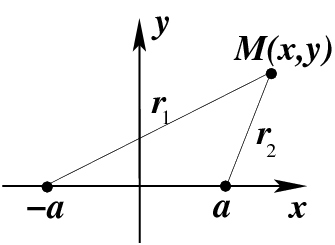
Эллиптическая система координат (на плоскости) определяется следующим образом. Рассмотрим
на плоскости
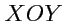
точку
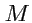
. На оси
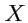
выберем два центра с координатами
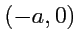
и
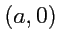
.
Соединим эти центра с точкой
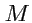
отрезками длиной
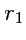
и
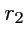
(рис.
42). Тогда
эллиптическими координатами точки
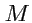
называются числа
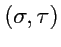
, определяемые как:
![$\displaystyle \left\{\begin{array}{l} \sigma=\displaystyle{\frac{r_1+r_2}{2a}}\\ [0.5em] \tau =\displaystyle{\frac{r_1-r_2}{2a}}\\ \end{array} \right.$](img968.png) |
(222) |
Рис.42 К определению эллиптической системы координат
Переходя к декартовым координатам
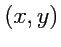
можно получить уравнения связи:
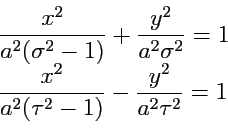 |
(223) |
c
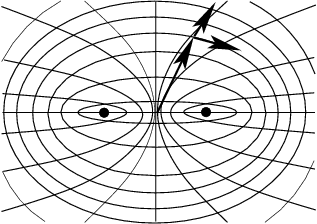
Рис.43 Эллиптическая система координат
и, таким образом, координатная сетка представляет собой семейство эллипсов
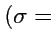
Const
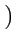
и гипербол
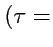
Const
с общими фокусами в точках
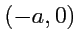
и
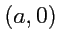
(рис.
43).
Пространственная эллиптическая система координат получается вращением (рис.
43) вокруг
оси
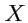
. В этом случае координатные поверхности будут софокусными эллипсоидами и гиперболоидами
вращения, а также плоскостями, проходящими через ось
.
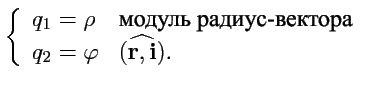

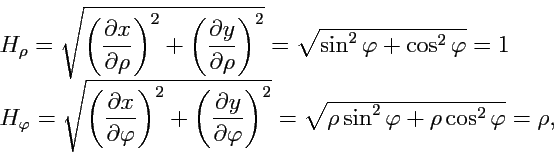
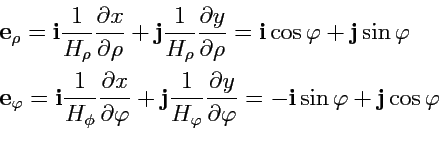
![$\displaystyle \hspace{-0.3em} \left\{\begin{array}{l} x = \rho\cos\varphi\\ [0....
...phi = \arctg\displaystyle{\frac{y}{x}}\\ [0.5em] z = z\\ \end{array}\ . \right.$](img941.png)
![$\displaystyle \left\{\begin{array}{l} {\mathbf e}_\rho = {\mathbf i}\cos\varphi...
...athbf j}\cos\varphi\\ [0.5em] {\mathbf e}_z = {\mathbf k}\\ \end{array} \right.$](img945.png)
![$\displaystyle \left\{\begin{array}{l} H_r = 1\\ [0.5em] H_\theta = r\\ [0.5em] H_\varphi = r\sin\theta.\\ \end{array} \right.$](img957.png)
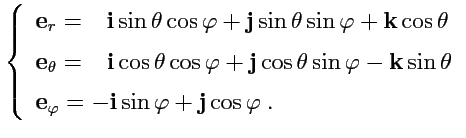
![$\displaystyle \left\{\begin{array}{l} \sigma=\displaystyle{\frac{r_1+r_2}{2a}}\\ [0.5em] \tau =\displaystyle{\frac{r_1-r_2}{2a}}\\ \end{array} \right.$](img968.png)