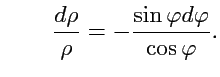Ранее было показано, что согласно определению векторной линии поля
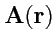
, ее уравнение
в бескоординатной форме имеет вид:
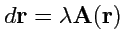
. Учитывая, что в криволинейной
системе
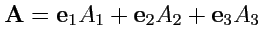
, а дифференциал вектора определяется
выражением (
204), получим:
Выражение (
224) называется уравнением векторных линий поля
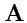
в криволинейной ортогональной системе
координат.
В качестве иллюстрации рассмотрим плоское поле
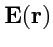
в полярной системе координат. Учитывая, что
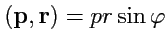
, а
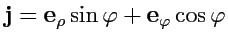
, получим
Окончательно уравнение векторных линий поля
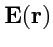
принимает вид:
которое определяет в плоскости
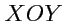
семейство окружностей радиуса
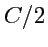
с общей точкой в начале
координат. Отметим, что в отличие от декартовой системы координат, в данном
случае, при использовании полярной, дифференциальное уравнение векторных линий интегрируется
элементарно.
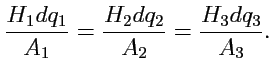
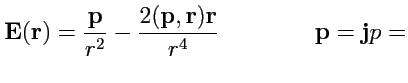 Const
Const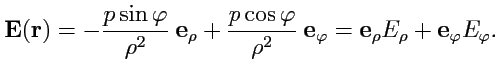
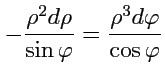 или
или