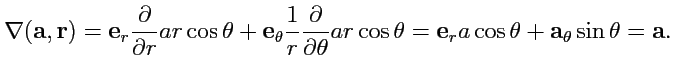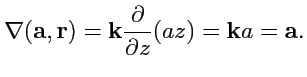4. Векторный анализ в криволинейных координатах
 4.6. Градиент, дивергенция, ротор в криволинейных ортогональных системах координат
4.6. Градиент, дивергенция, ротор в криволинейных ортогональных системах координат 
Ранее были даны бескоординатные, общие определения основных дифференциальных операций:
градиент, дивергения, ротор, а также на этой основе получены формулы (
79),
(
90), (
106), определяющие способ их вычисления в декартовой системе
координат. Однако, общее определение позволяет получить выражения для
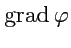
,
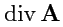
и
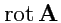
в произвольной системе координат.
1.
Градиент скалярного поля. Пусть дано скалярное поле

. Согласно
(
75),
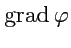
определяется как предел:
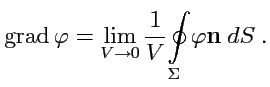 |
(225) |
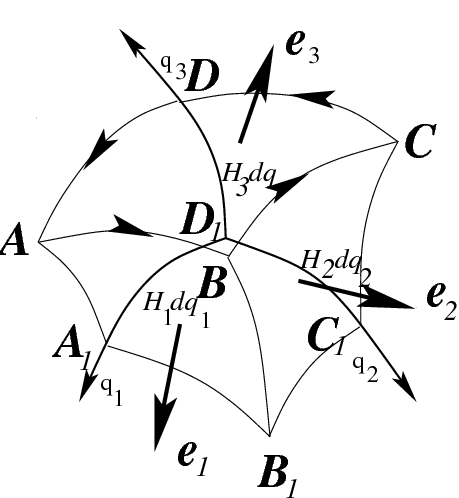
Рис.44 У вычислению интегралов вида (
225)
Пусть также в области определения поля

задана криволинейная ортогональная
система координат. Рассмотрим в качестве поверхности в (
225) бесконечно малый
параллелепипед объема
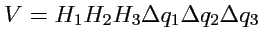
(рис.
44) (его
гранями будут координатные поверхности). Тогда, в силу малости этого параллелепипеда, нормаль
к каждой грани будет совпадать с соответствующим вектором репера:
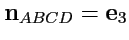
и т. д. Учитывая, что, например, на грани
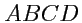
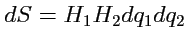
и аналогично на остальных,
получим:
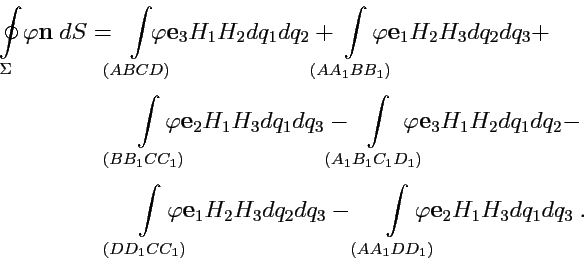 |
(226) |
Знак "минус" в последних трех слагемых появляется так как нормаль должна быть направлена
во внешнюю область замкнутой поверхности.
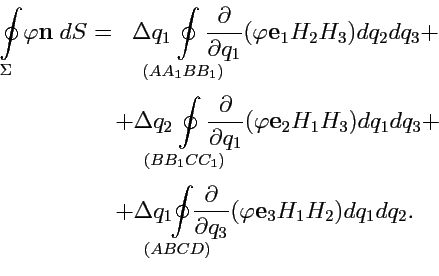 |
(227) |
Применяя теорему о среднем к (
227), переходим к пределу в (
225):
![\begin{displaymath}\begin{array}{l} {\rm grad}\,\varphi = \displaystyle{\frac{1}...
...{\partial q_3}}(\varphi{\mathbf e}_3H_1H_2) \biggr] \end{array}\end{displaymath}](img993.png) |
(228) |
![\begin{displaymath}\begin{array}{l} {\rm grad}\,\varphi = \biggl[{\mathbf e}_1\d...
...tial }{\partial q_3}}({\mathbf e}_3H_1H_2) \biggr]. \end{array}\end{displaymath}](img994.png) |
(229) |
Так как
![$ {\mathbf e}_3=[{\mathbf e}_1,{\mathbf e}_2]$](img995.png)
,
![$ {\mathbf e}_1=[{\mathbf e}_2,{\mathbf e}_3]$](img996.png)
,
![$ {\mathbf e}_2=[{\mathbf e}_3,{\mathbf e}_1]$](img997.png)
и
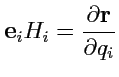
, то второе слагаемое в
(
229) преобразуется к виду:
и обращается в ноль по свойству смешанных производных. Таким образом, формула для вычисления
градиента скалярной функции в криволинейной ортогональной системе координат принимает вид:
![$\displaystyle {\rm grad}\,\varphi = \biggl[{\mathbf e}_1\displaystyle{\frac{1}{...
...e{\frac{1}{H_3}}\displaystyle{\frac{\partial \varphi}{\partial q_3}} \biggr]\ .$](img1000.png) |
(230) |
2.
Дивергенция векторного поля. Получим выражение для
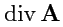
, используя общее
определение дивергенции, как предела:
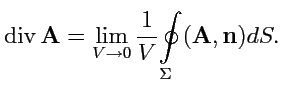 |
(231) |
Как и в первом случае, пусть объем
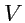
ограничен бесконечно малым параллелепипедом
(рис.
44). Вычислим поток в (
231):
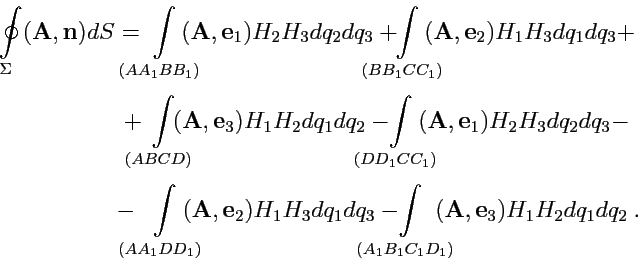 |
(232) |
Учитывая, что в ортогональной системе координат
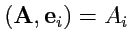
, получим
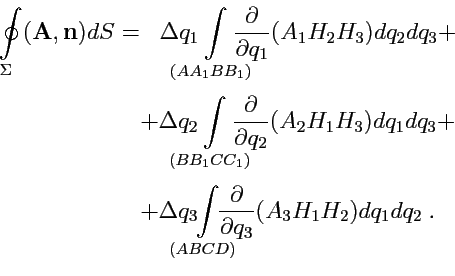 |
(233) |
Применяя теорему о среднем и переходя к пределу (
231), получим:
div![$\displaystyle {\mathbf A}=\displaystyle{\frac{1}{H_1H_2H_3}} \biggl[ \displayst...
...artial q_2}} + \displaystyle{\frac{\partial (H_1H_2A_3)}{\partial q_3}} \biggr]$](img1005.png) |
(234) |
3.
Ротор векторного поля. Согласно определению (
103), проекция вектора
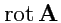
на произвольный вектор

равна:
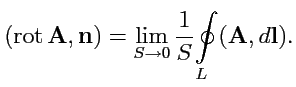 |
(235) |
Если в качестве

выбрать векторы репера
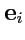
, то величины
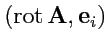
будут координатами вектора
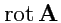
в системе координат, задаваемой тройкой
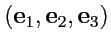
, т. е.

. Найдем
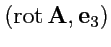
. Для
этого вычислим циркуляцию поля
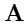
по контуру
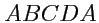
(рис.
44). Тогда
![\begin{displaymath}\begin{array}{ll} \displaystyle{\oint\limits_{(ABCDA)}}\hspac...
...laystyle{\int\limits_{(DA)}}(A_1H_1)dq_1\ .\\ [1em] \end{array}\end{displaymath}](img1011.png) |
(236) |
Учитывая, что на линии


,
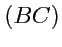
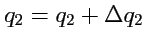
, вместе с теоремой
о среднем для каждого участка контура, получим:
![$\displaystyle \displaystyle{\oint\limits_{(ABCDA)}}\hspace{-1.0em}({\mathbf A},...
... q_1}}(A_2H_2) - \displaystyle{\frac{\partial }{\partial q_2}}(A_1H_1) \right].$](img1016.png) |
(237) |
Аналогичные вычисления можно проделать для векторов
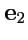
,
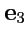
и тогда из
(
235) следует:
![\begin{displaymath}\begin{array}{c} ({\rm rot}\,{\mathbf A})_3 = \displaystyle{\...
...partial }{\partial q_2}}(A_1H_1) \right]\ .\\ [1em] \end{array}\end{displaymath}](img1018.png) |
(238) |
Так как
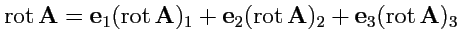
,
то (
238) можно переписать следующим образом:
![$\displaystyle {\rm rot}\,{\mathbf A} = \displaystyle{\frac{1}{H_1H_2H_3}} \left...
...{\partial q_3}} \\ [2em] A_1H_1 & A_2H_2 & A_3H_3 \\ \end{array} \right\vert\ .$](img1020.png) |
(239) |
4.
Оператор Лапласа определяется как
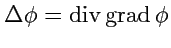
. Тогда, используя
выражения (
230) и (
234), получим:
![$\displaystyle \Delta\phi=\displaystyle{\frac{1}{H_1H_2H_3}} \left[ \displaystyl...
...H_1H_2}{H_3}}\displaystyle{\frac{\partial \phi}{\partial q_1}} \right) \right].$](img1022.png) |
(240) |
С использованием общих выражений для

,
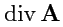
,
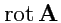
и
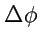
можно
получить следующие формулы для вычисления в:
-
цилиндрической системе координат
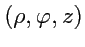
:
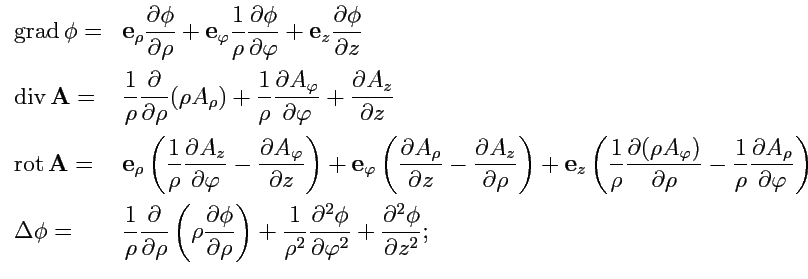 |
(241) |
-
сферической системе координат
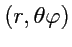
:
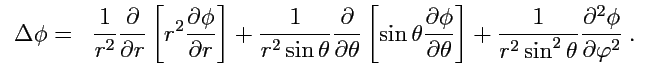 |
(242) |
Пример 4-1. Вычислить
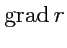
,

и

в сферической системе координат.
Решение. Радиус-вектор в сферической системе координат имеет вид
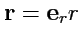
,
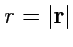
и
тогда
Пример 4-2. Вычислить
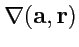
,
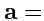
Const.
Решение. Направим ось
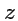
вдоль вектора
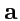
. Тогда в сферической системе координат
В цилиндрической системе координат
Как видно, цилиндрическая система координат в данном случае "выгоднее" сферической, что
определяется свойством дифференцируемой функции, которая имеет цилиндрическую симметрию за счет выделенного направления, заданного вектором
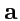
.
![]() 4.6. Градиент, дивергенция, ротор в криволинейных ортогональных системах координат
4.6. Градиент, дивергенция, ротор в криволинейных ортогональных системах координат ![]()
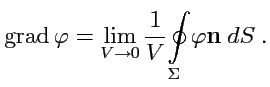
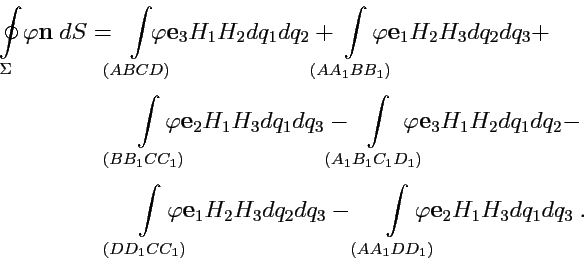
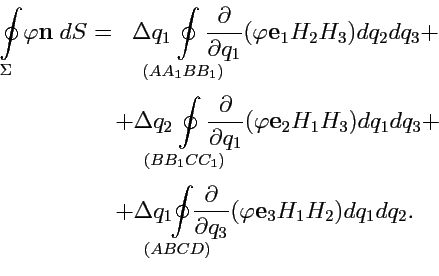
![\begin{displaymath}\begin{array}{l} {\rm grad}\,\varphi = \displaystyle{\frac{1}...
...{\partial q_3}}(\varphi{\mathbf e}_3H_1H_2) \biggr] \end{array}\end{displaymath}](img993.png)
![$\displaystyle {\rm grad}\,\varphi = \biggl[{\mathbf e}_1\displaystyle{\frac{1}{...
...e{\frac{1}{H_3}}\displaystyle{\frac{\partial \varphi}{\partial q_3}} \biggr]\ .$](img1000.png)
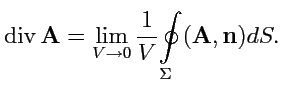
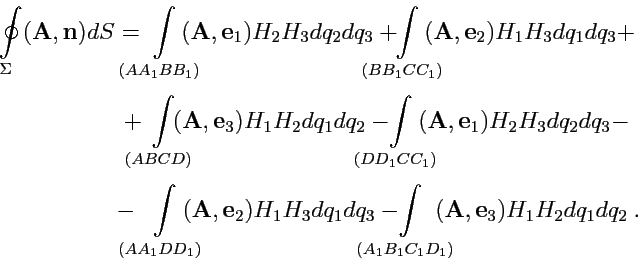
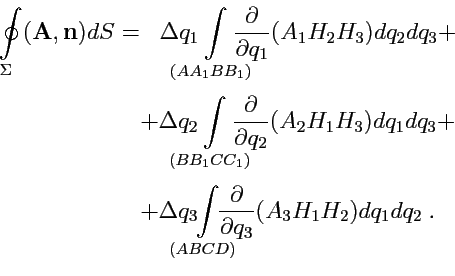
![$\displaystyle {\mathbf A}=\displaystyle{\frac{1}{H_1H_2H_3}} \biggl[ \displayst...
...artial q_2}} + \displaystyle{\frac{\partial (H_1H_2A_3)}{\partial q_3}} \biggr]$](img1005.png)
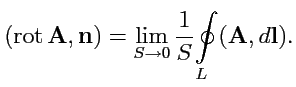
![\begin{displaymath}\begin{array}{ll} \displaystyle{\oint\limits_{(ABCDA)}}\hspac...
...laystyle{\int\limits_{(DA)}}(A_1H_1)dq_1\ .\\ [1em] \end{array}\end{displaymath}](img1011.png)
![$\displaystyle \displaystyle{\oint\limits_{(ABCDA)}}\hspace{-1.0em}({\mathbf A},...
... q_1}}(A_2H_2) - \displaystyle{\frac{\partial }{\partial q_2}}(A_1H_1) \right].$](img1016.png)
![$\displaystyle {\rm rot}\,{\mathbf A} = \displaystyle{\frac{1}{H_1H_2H_3}} \left...
...{\partial q_3}} \\ [2em] A_1H_1 & A_2H_2 & A_3H_3 \\ \end{array} \right\vert\ .$](img1020.png)
![$\displaystyle \Delta\phi=\displaystyle{\frac{1}{H_1H_2H_3}} \left[ \displaystyl...
...H_1H_2}{H_3}}\displaystyle{\frac{\partial \phi}{\partial q_1}} \right) \right].$](img1022.png)
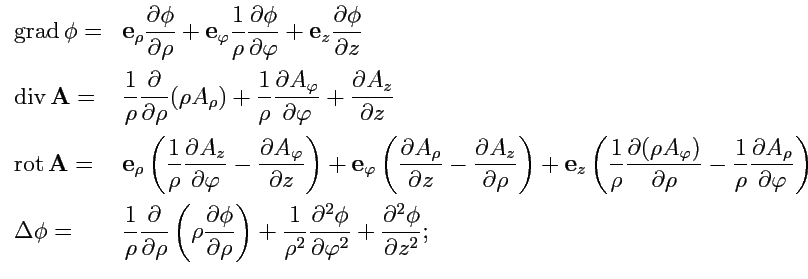
![\begin{displaymath}
{\normalsize
\begin{array}{ll}
{\rm grad}\,\phi = & {\mathbf...
...partial A_r}{\partial \theta}}
\right] \\ [1em]
\end{array}}
\end{displaymath}](img1026.png)
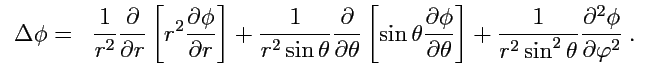
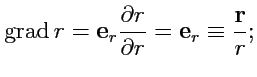
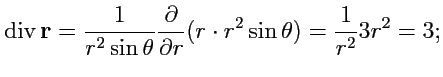
![\begin{displaymath}
{\rm rot}\,{\mathbf r} = \displaystyle{\frac{1}{r^2\sin\thet...
...l \varphi}} \\ [1em]
r & 0 & 0 \\
\end{array}\right\vert = 0.
\end{displaymath}](img1034.png)