5. Основы тензорного анализа
 5.15. Тензоры общего вида
5.15. Тензоры общего вида 
Наряду с рассмотренными ко- и контравариантными тензорами существуют тензоры, которые одновременно
являются и ковариантными, и контравариантными. Например, рассмотрим правило, сопоставляющее каждому
вектору
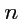
-мерного пространства новый вектор
 |
(312) |
Такое правило называется
оператором или
аффинором, а вычисление результата, т. е. вектора
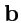
, - действием оператора
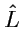
на вектор
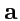
. Пусть правило (
312) обладает
свойством линейности
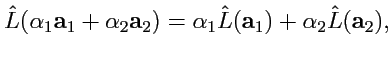 |
(313) |
где
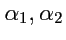
- числа. Подействуем оператором
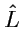
на базисный вектор
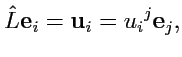 |
(314) |
где
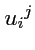
- контравариантные координаты вектора
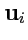
. Тогда, согласно (
312) и
(
314)
 |
(315) |
т. е. координаты нового вектора, который получается из вектора
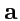
действием оператора
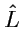
и самого вектора
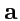
, связаны соотношением
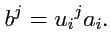 |
(316) |
Из (
316) видно, что коэффициенты разложения всех базисных векторов
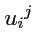
полностью
определяют способ вычисления результатов действия оператора
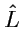
в (
312). Эти коэффициенты,
по аналогии с векторами назовем координатами оператора. Поскольку координаты оператора "привязаны" к соответствующему базису
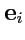
, то изменение этого базиса будет вызывать и изменение
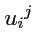
. Действительно
 |
(317) |
и тогда, с одной стороны, выражая

через
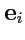
и учитывая линейность
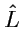
,
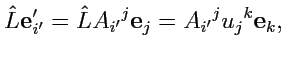 |
(318) |
а с другой, после преобразования правой части (
317)
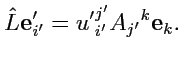 |
(319) |
Приравнивая коэффициенты при одинаковых базисных векторах в (
318) и (
319),
получим:
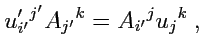 |
(320) |
откуда можно окончательно выразить
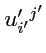
через
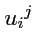
:
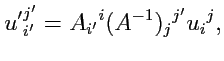 |
(321) |
что дает закон преобразования координат оператора (аффинора). Из (
321) видно,
что один индекс (
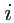
) преобразуется по ковариантному закону, а другой

- по контравариантному.
Совокупность координат

оператора
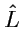
, заданного в каждом базисе (и сам оператор)
называют тензором ранга 2, один раз ковариантным и один раз контравариантным
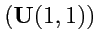
.
Отметим важный случай тождествнного (единичного) оператора:
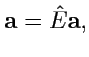 |
(322) |
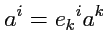 |
(323) |
и, сравнивая (
323) с определением дельта-символа, находим
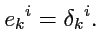 |
(324) |
Единичный оператор является примером инвариантного тензора ранга 2, один раз ковариантного и один
раз контравариантного. Свойство инвариантности следует из закона преобразования координат единичного
оператора. Действительно, применяя закон преобразования (
321) для случая
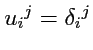
,
получим:
т. е. координаты единичного инвариантного тензора не зависят от выбора базиса.
Приведенные рассуждения и примеры позволяют дать общее определение тензора:
- тензором ранга

,
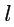
раз ковариантным и
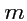
раз контравариантным, определенным в
линейном пространстве размерности
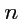
, называется объект
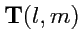
, который в любом базисе
задается числами, занумерованными
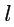
нижними и
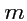
верхними индексами
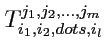
; в разных базисах эти наборы чисел разные, но их
значения связаны между собой с помощью
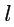
матриц
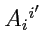
преобразования базиса и
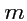
контрагредиентных матриц
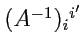
:
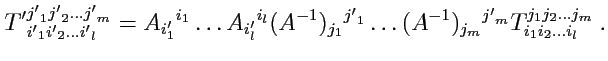 |
(325) |
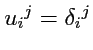 ,
получим:
,
получим:
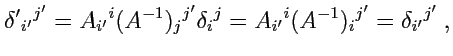
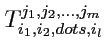 ; в разных базисах эти наборы чисел разные, но их
значения связаны между собой с помощью
; в разных базисах эти наборы чисел разные, но их
значения связаны между собой с помощью 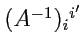 :
: