5. Основы тензорного анализа
 5.14. Понятие контравариантного тензора
5.14. Понятие контравариантного тензора 
Важным примером контравариантного тензора являются контравариантные координаты
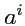
(
283)
фиксированного вектора

, преобразующиеся при изменении базиса согласно правилу (
293),
которое принимается за основу определения:
-контравариантным тензором ранга 1, определенным на линейном пространстве размерности

, называется
объект
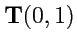
, который в любом базисе задается

числами, занумерованными верхними индексами -
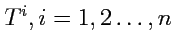
; в разных базисах эти числа связаны 1-ой матрицей, обратной и транспонированной
к матрице преобразования базисных векторов:
Можно рассмотреть два фиксированных вектора

и

и в выбранном базисе
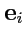
составить
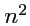
произведений их координат
При переходе к новому базису контравариантные координаты векторов

и

будут
изменяться согласно (
308), что для значений
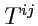
дает правило:
определяя, таким образом, понятие контравариантного тензора ранга 2. В общем случае:
- контравариантным тензором ранга
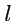
, определенным на линейном пространстве размерности

,
называется объект
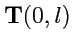
, который в любом базисе задается
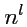
числами, занумерованными
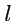
верхними индексами
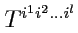
; в разных базисах эти наборы чисел разные, но их
значения связаны
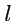
матрицами, обратными и транспонированными к матрице преобразования базисных
векторов
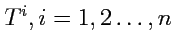 ; в разных базисах эти числа связаны 1-ой матрицей, обратной и транспонированной
к матрице преобразования базисных векторов:
; в разных базисах эти числа связаны 1-ой матрицей, обратной и транспонированной
к матрице преобразования базисных векторов: