5. Основы тензорного анализа
 5.13. Расширенное определение тензора
5.13. Расширенное определение тензора 
Рассмотрим линейную скалярную функцию с областью определения из

-мерного векторного пространства,
т. е. любому вектору

сопоставим в соответствие число
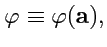 |
(297) |
причем
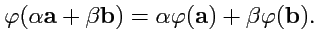 |
(298) |
Так как в выбранном базисе
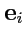
любой вектор определяется своими контравариантными координатами
(
283),то
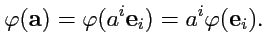 |
(299) |
Обозначим для краткости
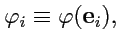 |
(300) |
тогда
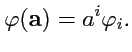 |
(301) |
Теперь выберем в этом же пространстве другой базис
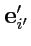
. Тогда разложение вектора-аргумента
скалярной функции (
297) изменится
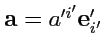
, но значение самой функции
остаетсяпрежним
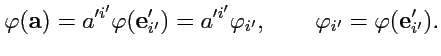 |
(302) |
Так как при переходе от одного базиса к другому контравариантные координаты преобразуются по закону
(
293), то значения функции на базисных векторах
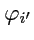
также должны изменяться,
чтобы обеспечить инвариантность значения
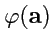
:
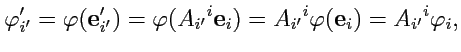 |
(303) |
т. е. эти величины преобразуются
точно так же, как и векторы базиса. Итак, если на линейном
пространстве задана линейная скалярная функция
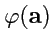
, то в каждом базисе возникают

чисел, которые преобразуются по такому же закону, что и векторы соответствующего базиса. Таким образом,
мы приходим к понятию ковариантного тензора ранга 1 (ковариантного вектора).
Определение: ковариантным тензором ранга 1, определенным на линейном пространстве размерности

, называется объект
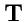
, который в любом базисе задается

числами, занумерованными нижними
индексами
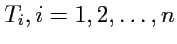
; в разных базисах наборы чисел
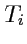
различны, но их значения связаны
1-ой матрицей преобразования базисных векторов
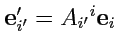
по тому же закону:
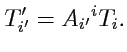 |
(304) |
Числа
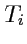
называются
ковариантными координатами тензора
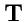
в соответствующем базисе.
Термин ковариантный, т. е.
сопреобразующийся, выражает то обстоятельство, что закон преобразования
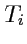
точно такой же, как и для векторов базиса. Примером ковариантного тензора 1-го ранга служит
линейная функция
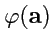
; верно и обратное - любой ковариантный тензор 1-го ранга можно
трактовать как линейную функцию.
Можно обобщить понятие ковариантного тензора, увеличив его ранг. Например, рассмотрим скалярную линейную
функцию двух векторных аргументов
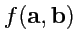
. Выбрав базис
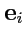
и учитывая линейность функции,
ее можно представить как
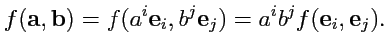 |
(305) |
Вводя
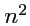
чисел
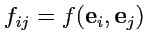
, можно легко показать, что они преобразуются по закону
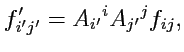 |
(306) |
который указывает на то, что объект
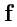
с компонентами
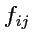
является ковариантным тензором
2-го ранга. В общем случае:
- ковариантным тензором ранга
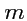
, определенным на линейном пространстве размерности

, называется
объект
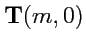
, который в любом базисе задается
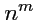
числами, которые удобно нумеровать нижними
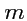
индексами
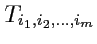
и которые в разных базисах связаны
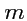
матрицами преобразования
базисных векторов по тому же самому закону:
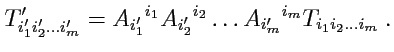 |
(307) |
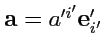 , но значение самой функции
остаетсяпрежним
, но значение самой функции
остаетсяпрежним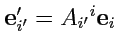 по тому же закону:
по тому же закону: