5. Основы тензорного анализа
 5.12. Обобщение понятия вектора
5.12. Обобщение понятия вектора 
Рассмотрим
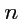
-мерное пространство, отказываясь от некоторых предположений, существенных
для векторов, как направленных отрезков в 3-х мерном пространстве. Будем считать, что дано
множество объектов, обозначаемых как
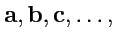
на котором определены
две операции: сложение -

и умножение на число (в общем случае комплексное)
-
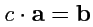
, удовлетворяющие
8 аксиомам линейного пространства.
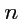
-мерность означает,
что на этом множестве существуют
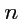
линейно независимых векторов
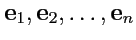
,
которые образуют базис, а любые
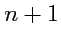
векторов будут линейно зависимы. В этом случае любой вектор
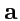
может быть однозначно представлен в виде линейной комбинации базисных векторов
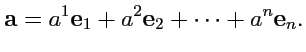 |
(282) |
Индексы, нумерующие базисные векторы, т. е.
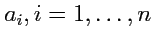
будем писать сверху
и называть
контравариантными, в отличие от
ковариантных индексов, которые принято писать
снизу. Как уже отмечалось ранее, многократные суммы в тензорной алгебре принято записывать в сокращенной
форме, используя правило Эйнштейна. Так как в выражении типа (
282) используется два типа индексов,
то упрощенное правило Эйнштейна должно быть расширено и теперь будем считать
суммируемыми
такие пары индексов, в которых один - верхний, а второй - обязательно нижний (или наоборот). Тогда
(
282)можно переписать в форме
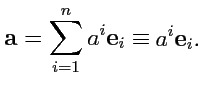 |
(283) |
Набор коэффициентов
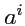
однозначно определяет любой вектор
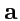
в выбранном базисе и называется
контравариантными координатами вектора
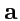
в базисе
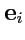
. Множество наборов контравариантных
координат само по себе образует линейное
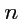
-мерное пространство, поскольку для таких составных объектов
определены операции сложения и умножения, отвечающие 8 аксиомам, и это пространство является изоморфным
исходному. Таким образом, координаты
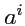
сами являются контравариантными векторами, в отличие от
ковариантного
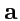
. Заметим, что линейные пространства ко- и контравариантных векторов - это разные
пространства с элементами разной природы.
Рассмотрим в исходном пространстве другой набор базисных векторов

. Так как
каждый из
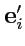
является
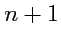
вектором в отношении набора
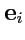
, то в силу линейной
зависимости набора
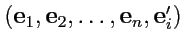
всегда можно выразить
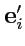
в виде линейной комбинации
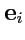
:
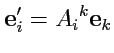 |
(284) |
или в матричной форме
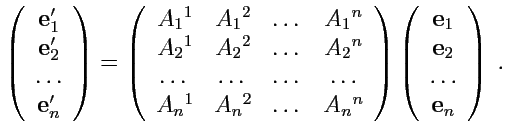 |
(285) |
Матрица
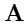
связывает два базисных набора и аналогична матрице ортогональных преобразований,
но теперь, согласно договоренности о правиле суммирования (
283), матричные элементы
необходимо нумеровать ко- и контравариантными индексами. Например, единичная матрица будет иметь
элементы:
![$\displaystyle \delta_i{}^j = \left\{\begin{array}{l} 1,\qquad i=j \\ [1em] 0,\qquad i\ne j, \\ \end{array} \right.$](img1185.png) |
(286) |
что определяет
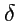
-символ Кронекера. Так как новые векторы (
284) линейно независимы,
то строки матрицы (
285) также линейно независимы и определитель матрицы (
285)
должен быть отличным от нуля:
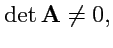 |
(287) |
что эквивалентно условию существования для матрицы
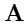
обратной матрицы

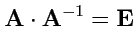 или или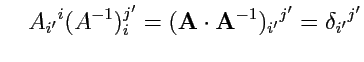 |
(288) |
(
288) является единственным условием, которое накладывается на преобразование векторов.
В остальном коэффициенты
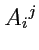
произвольны.
Если, наоборот, выразить векторы
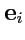
через
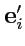
как
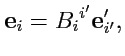 |
(289) |
то, используя (
284), получим для матрицы
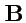
:
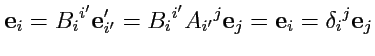 |
(290) |
т. е.
При переходе к новому базису
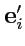
контравариантные координаты вектора
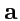
изменяются:
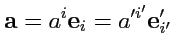 |
(291) |
и, используя связь между двумя базисами (
284),
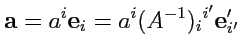 |
(292) |
откуда
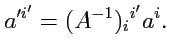 |
(293) |
Для того, чтобы записать выражение (
293) в матричном виде, необходимо учесть, что при
использовании "ступенчатой" индексации верхний правый индекс в выражении
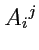
по смыслу
правила матричного умножения должен рассматриваться как номер столбца и тогда аналог формулы (
285),
но для преобразования координат вектора
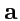
, принимает вид:
 |
(294) |
Аналогично можно получить и обратное преобразование контравариантных координат
 |
(295) |
Весьма важно сравнить формулы преобразования базисных ковариантных векторов (
284)
и (
294)
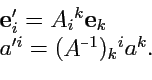 |
(296) |
Видно, что матрицы этих преобразований различны, а именно матрица преобразования координат
является
транспонированной обратной по отношению к матрице преобразования самих векторов -
такие преобразования называются также
контрагредиентными преобразованиями. Отсюда и происходит
название
контравариантные координаты, т. е.
противопреобразующиеся по сравнению с
преобразованиями базисных векторов. Отметим, что ортонормированные базисные векторы как направленные
отрезки, рассматриваемые в Главе 1, преобразуются с помощью ортогональной матрицы, для которой
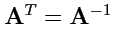
и соответственно
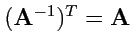
, т. е. контрагредиентное
преобразование совпадает с исходным. В этом случае нет различий в способах преобразования
базисных векторов и координат произвольных векторов и необходимости различать типы величин с
помощью разных типов индексов, т. е. ко- и контравариантных, не возникало.
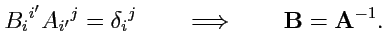
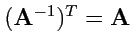 , т. е. контрагредиентное
преобразование совпадает с исходным. В этом случае нет различий в способах преобразования
базисных векторов и координат произвольных векторов и необходимости различать типы величин с
помощью разных типов индексов, т. е. ко- и контравариантных, не возникало.
, т. е. контрагредиентное
преобразование совпадает с исходным. В этом случае нет различий в способах преобразования
базисных векторов и координат произвольных векторов и необходимости различать типы величин с
помощью разных типов индексов, т. е. ко- и контравариантных, не возникало.