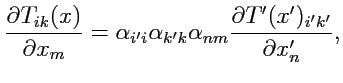Тензорные поля

5. Основы тензорного анализа

5.11. Тензорные поля

Если каждой точке пространства или некоторой его области однозначно соответствует некоторый тензор ранга

, то говорят, что задано тензорное поле ранга . Частные случаи тензорных полей уже были рассмотрены ранее - скалярное поле как тензорное поле ранга ноль, векторное поле как тензорное поле ранга 1. Тензорные поля, которые меняются со временем, называются нестационарными.

Далее будут рассматриваться непрерывные тензорные поля, т. е. такие что

$\displaystyle \lim_{\vert\Delta{\mathbf r}\to 0\vert}\biggl[ T_{\dots i\dots k\... ...thbf r}+\Delta{\mathbf r})- T_{\dots i\dots k\dots}({\mathbf r}) \biggr] = 0.$

Для тензорных полей справедливы все операции тензорной алгебры, при этом, естественно, все действия (сложение, умножение, свертка) должны производиться в фиксированной точке пространства.

Рассмотрим простейшие свойства тензорных полей:

дифференцирование тензорного поля по скалярному аргументу не меняет его ранг. Справедливость этого утверждения следует из определения производной

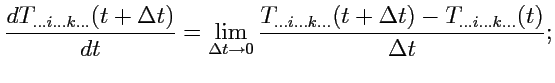
$\displaystyle \displaystyle{\frac{dT_{\dots i\dots k\dots}(t+\Delta t)}{dt}} = ... ...{T_{\dots i\dots k\dots}(t+\Delta t)- T_{\dots i\dots k\dots}(t)}{\Delta t}};$
однократное дифференцирование тензорного поля по координатам радиус-вектора увеличивает его ранг на единицу.

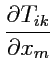Действительно, рассмотрим тензорное поле второго ранга $T_{ik}(x,y,z)\equiv T_{ik}(x_1,x_2,x_3)$ , образуем из его компонент совокупность всевозможных частных производных $\displaystyle{\frac{\partial T_{ik}}{\partial x_m}}$ и рассмотрим закон преобразования: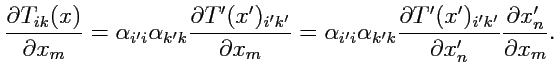

$\displaystyle \displaystyle{\frac{\partial T_{ik}(x)}{\partial x_m}} = \alpha_{... ...(x')_{i'k'}}{\partial x'_n}}\displaystyle{\frac{\partial x'_n}{\partial x_m}}.$

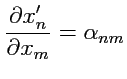Так как $x'_n=\alpha_{nn'}x_{n'}$ , то $\displaystyle{\frac{\partial x'_n}{\partial x_m}}=\alpha_{nm}$ , тогда

$\displaystyle \displaystyle{\frac{\partial T_{ik}(x)}{\partial x_m}} = \alpha_{... ...a_{k'k}\alpha_{nm}\displaystyle{\frac{\partial T'(x')_{i'k'}}{\partial x'_n}},$

что и требовалось доказать.


			Содержание