Над псевдотензорами можно производить такие же алгебраические операции, как и над истинными (полярными) тензорами : сложение, умножение, свертку. При этом следует учитывать, что

1. Сумма псевдотензоров одинакового ранга является псевдотензором того же ранга;
2. Сумма тензора и псевдотензора не является ни тензором ни псевдотензором. Такая величина преобразуется как тензор только при поворотах (собственных преобразованиях) систем координат;
3. произведение псевдотензора на псевдотензор является тензором;
4. произведение псевдотензора на тензор является псевдотензором.

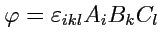
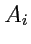
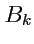
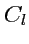
      Пример 5-3. Величина , где , , - компоненты векторов (тензоров 1-го ранга), согласно алгебре псевдотензоров является псевдоскаляром, так как операция умножения дает псевдотензор 6-го ранга, а три сверки далее понижают ранг до нуля. Из определения (16) следует, что этот скаляр является смешанным произведением