Единичный псевдотензор Леви-Чивиты

5. Основы тензорного анализа

5.9. Единичный псевдотензор Леви-Чивиты

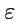
Важным примером псевдотензора является $\varepsilon$ -символ, определяемый соотношениями (14), (16), (17). Из формулы (16) следует, что при собственных преобразованиях (поворотах системы координат)

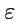
$\displaystyle \varepsilon'_{klm} = ({\mathbf e}'_k,[{\mathbf e}'_l,{\mathbf e}'... ... ({\mathbf e}_{k'},[{\mathbf e}_{l'},{\mathbf e}_{m'}]) = \varepsilon_{k'l'm'}$

и $\varepsilon$ -символ ведет себя как тензор ранга 3.

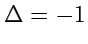
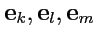
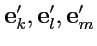
Рассмотрим теперь преобразование с $\Delta=-1$ , например, преобразование инверсии, матрица которого имеет вид (34). В этом случае правая тройка ${\mathbf e}_k, {\mathbf e}_l, {\mathbf e}_m$ переходит в левую ${\mathbf e}'_k, {\mathbf e}'_l,{\mathbf e}'_m$ , при этом

$\displaystyle ({\mathbf e}'_k,[{\mathbf e}'_l,{\mathbf e}'_m]) = I_{kk'} I_{ll'} I_{mm'} ({\mathbf e}_{k'},[{\mathbf e}_{l'},{\mathbf e}_{m'}]),$

(280)

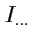
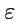
где $I_{...}$ - матрицы (34). Но $\varepsilon$ -символ определен в правой системе координат, поэтому $({\mathbf e}'_k,[{\mathbf e}'_l,{\mathbf e}'_m])=-\varepsilon'_{klm}$ и следовательно (280) можно переписать в виде

$\displaystyle \varepsilon'_{klm} = - I_{kk'} I_{ll'} I_{mm'} ({\mathbf e}_{k'},... ..._{l'},{\mathbf e}_{m'}]) = \Delta I_{kk'} I_{ll'} I_{mm'} \varepsilon_{k'l'm'}.$

(281)

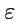
Таким образом, $\varepsilon$ -символ является псевдотензором 3-го ранга.


			Содержание