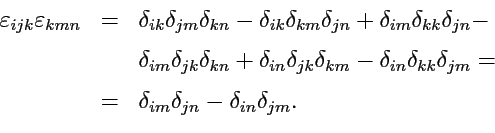1. Основные сведения из векторной алгебры
 1.8. Эпсилон-символ Леви-Чивиты.
1.8. Эпсилон-символ Леви-Чивиты. 
"Эпсилон"-символом Леви-Чивиты называется величина
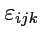
, определенная
следующим образом:
 |
(14) |
Напомним, что перестановкой чисел
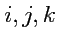
- обозначено как
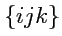
- называется последовательность
из трех разных чисел 1, 2 и 3, записанная в произвольном порядке,
например,

. Четность перестановки
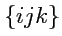
определяется числом "переставлений" пар
чисел, после которых
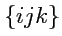
приводится к стандартной

: если это число
четное,
то и перестановка называется четной и наоборот. Например, перестановка

- нечетная,
так как

получается после 1 переставления чисел 3 и 2. Как следует из определения (
14),
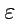
-символ Леви-Чивиты - это величина,
задаваемая
27 числами (индексы
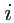
,
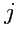
,
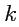
принимают значения 1, 2, 3), среди которых
3 равны единице
три - (
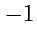
)
и остальные равны нулю, поскольку все другие комбинации будут содержать два или три равных
значений индексов.
С использованием определения можно в краткой форме записать систему (
3), определяющую
"правый" декартовый базис
![$\displaystyle [{\mathbf e}_k,{\mathbf e}_l] = \varepsilon_{klm}{\mathbf e}_m.$](img197.png) |
(15) |
Действительно, проверим (
15) для ортов

и
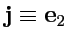
:
Если правую и левую части (
15) умножить скалярно на орт
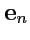
, то получим
Таким образом, эквивалентное определение для
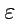
-символа Леви-Чивиты можно дать
с помощью смешанного произведения ортов декартового базиса в 3-х мерном пространстве:
![$\displaystyle \varepsilon_{ijk}=([{\mathbf e}_i,{\mathbf e}_j],{\mathbf e}_k).$](img203.png) |
(16) |
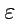
-символ связан с векторным или смешанным произведением, но кроме того он может
быть выражен с помощью
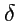
-символа. Действительно,
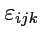
можно записать
в виде определителя
![$\displaystyle \varepsilon_{ijk}=\left\vert\begin{array}{ccc} \delta_{i1} & \del...
... \\ [0.5em] \delta_{k1} & \delta_{k2} & \delta_{k3} \\ \end{array} \right\vert.$](img204.png) |
(17) |
Форма следует из (
16) после подстановки координат базисных векторов,
выраженных с помощью
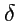
-символов, а с другой стороны (
17) также
можно рассматривать и как независимое определение
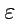
-символа.
Для иллюстрации работы с
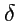
- и
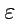
-символами рассмотрим несколько важных
для дальнейшего изложения примеров.
Пример 1-2. Показать,что
![$\displaystyle \varepsilon_{ijk}\varepsilon_{lmn} = \left\vert\begin{array}{ccc}...
... \\ [0.5em] \delta_{kl} & \delta_{km} & \delta_{kn} \\ \end{array} \right\vert.$](img205.png) |
(18) |
Решение. Обозначим матрицу, определитель которой стоит в правой части (
18) через
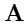
, т. е.
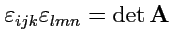
. Аналогично,
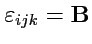
,

, где матрицы
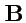
и
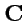
определяются согласно (
17). Воспользуемся свойствами определителей:
- определитель матрицы
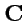 и транспонированной матрицы
и транспонированной матрицы
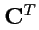 совпадают:
совпадают:
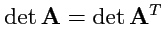 ;
;
- определитель произведения матриц равен произведению определителей матриц-сомножителей:
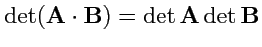 ;
;
Тогда, (
18) можно переписать в виде:
Элемент матрицы произведения
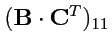
равен
и продолжая аналогично, получим
что и требовалось доказать.
Пример 1-3. Доказать тождество
Решение. Воспользуемся результатом предыдущего примера, тогда
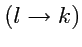
:
и после раскрытия определителя, учитывая, что сумма
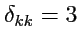
, получим:
Пример 1-4. Вычислить двойную сумму
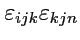
.
Решение. Используем результат
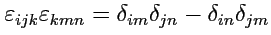
, тогда,
заменяя индекс

,
Отсюда, в частности, следует, что
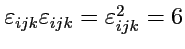
.
Пример 1-5. Определитель
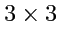
матрицы

может быть записан в виде
:
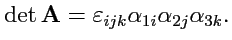 |
(19) |
(доказать самостоятельно !)
![$\displaystyle {\mathbf B}\cdot{\mathbf C}^T =
\left(\begin{array}{ccc}
\delta_...
...n2} \\ [0.5em]
\delta_{l3} & \delta_{m3} & \delta_{n3} \\
\end{array}\right).
$](img215.png)
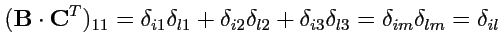
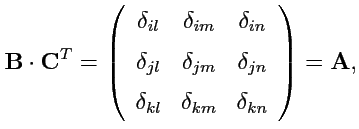
![$\displaystyle \varepsilon_{ijk}\varepsilon_{kmn} =
\left\vert\begin{array}{ccc...
...\ [0.5em]
\delta_{kk} & \delta_{km} & \delta_{kn} \\
\end{array}
\right\vert
$](img221.png)