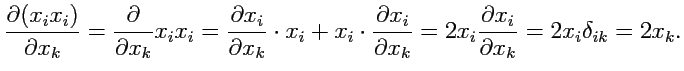1. Основные сведения из векторной алгебры
 1.7. Дельта-символ Кронекера.
1.7. Дельта-символ Кронекера. 
В этом и следующем разделах будет дано "конструктивное" определение часто встречающихся
величин с индексами с целью более глубокого понимания особенностей их использования.
Дельта-символом Кронекера
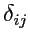
называется величина, которая определяется как
![$\displaystyle \delta_{ik} = \left\{ \begin{array}{ll} 1, & \mbox{если} i=k \\ [0.5em] 0, & \mbox{если} i\ne k. \\ [0.5em] \end{array} \right.$](img166.png) |
(11) |
Фактически, это величина, задаваемая 9-ю числами, три из которых равны 1, а остальные нули.
Записывая все значения дельта-символа в соответствии с обозначением элементов матрицы, получим
![$\displaystyle (\delta) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ [0.5em] 0 & 1 & 0 \\ [0.5em] 0 & 0 & 1 \\ [0.0em] \end{array} \right).$](img167.png) |
(12) |
Таким образом,
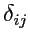
это обозначение произвольного элемента единичной матрицы. Используя
определение (
11), можно записать условие ортонормировки декартового базиса (
1)
в сокращенном виде
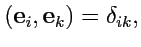 |
(13) |
заменив, таким образом, девять равенств (
1) только одним.
Как уже указывалось, любой вектор может быть разложен по базисным векторам, например, по
декартовому базису

. Разложим по этому базису, например, вектор
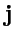
. Очевидно, что
т. е. вектор
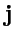
в своем базисе имеет координаты

. Зададимся вопросом: какие
координаты будет иметь произвольный базисный вектор в своем базисе.
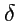
-символ
позволяет ответить на этот вопрос: координаты вектора

будут выражаться тройкой
чисел
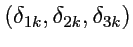
. Таким образом,
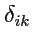
- это
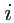
-тая координата
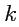
-того орта (или наоборот) в своем базисе.
Главной особенностью
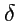
-символа Кронекера является то, что он "снимает" суммирование.
Рассмотрим сумму
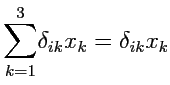
. Сгруппируем слагаемые этой суммы
следующим образом
т. е. в одном лишь слагаемом значение индекса суммирования стало равным значению
"внешнего" для этой суммы значения (
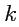
). Поскольку, согласно определению (
11),
все значения
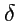
-символа в первом слагаемом (сумме) равны нулю, то
Таким образом, окончательно результат суммирования имеет вид:
Полученный результат позволяет сформулировать общее правило "снятия" сумм:
при суммирования с 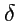 -символом, сумма по "бегущему" индексу
-символом, сумма по "бегущему" индексу 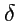 -символа
снимается, а все остальные индексы в выражении заменяются на его "свободный"
-символа
снимается, а все остальные индексы в выражении заменяются на его "свободный".
Напомним, что в рассмотренном выше примере, "бегущим" индексом
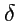
-символа является
индекс
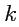
, "свободным" -
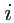
.
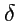
-символ естественным оборазом возникает в скалярных произведениях декартовых ортов,
(
13), а другой путь получения
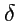
-символа связан с дифференцированием по
координатам. Рассмотрим производную координаты
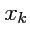
(как функции) по координате (как
переменной)
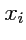
, т. е.
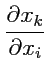
. Очевидно, что результат равен единице, если

,
и нулю - при
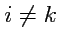
и, таким образом,
Пример 1-1. Вычислить производную
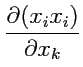
.
Решение.
![$\displaystyle (\delta) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ [0.5em] 0 & 1 & 0 \\ [0.5em] 0 & 0 & 1 \\ [0.0em] \end{array} \right).$](img167.png)
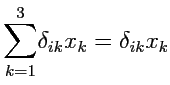 . Сгруппируем слагаемые этой суммы
следующим образом
. Сгруппируем слагаемые этой суммы
следующим образом
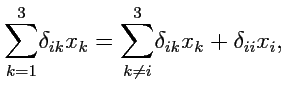
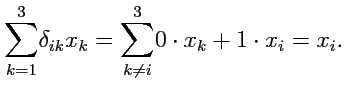
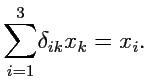
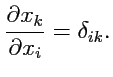
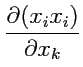 .
.