1. Основные сведения из векторной алгебры

Векторный базис 1.6. Декартов базис Дельта-символ Кронекера


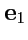
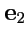
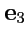
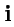
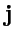
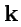
      Если векторы $ {\mathbf e}_1$, $ {\mathbf e}_2$, $ {\mathbf e}_3$ взаимно ортогональны и по модулю равны единице, то они называются ортами прямоугольной декартовой системы координат, а сам базис ортонормированным декартовым базисом. Орты декартовой системы координат обычно обозначают как $ {\mathbf i}$, $ {\mathbf j}$, $ {\mathbf k}$. Согласно определению

$\displaystyle ({\mathbf i},{\mathbf i})=({\mathbf j},{\mathbf j})=({\mathbf k},... ...mathbf i},{\mathbf j})=({\mathbf i},{\mathbf k})=({\mathbf j},{\mathbf k}) = 0.$ (1)

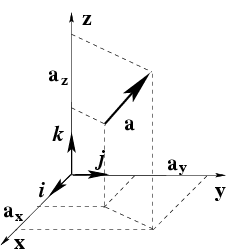
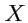
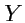
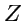
Главная особеннность декартовых базисов состоит в том, что координаты любого вектора в этом базисе равны проекциям этого вектора на три взаимно ортогональных направления, определяемых ортами. Эти направления называют координатными осями декартовой системы координат (рис. 9): оси $ X$, $ Y$ и $ Z$. Точка пересечения координатных осей 0 называется началом координат. Тогда
Рис.9 Декартова система координат

$\displaystyle {\mathbf a}={\mathbf i}a_x + {\mathbf j}a_y + {\mathbf k} a_z, $
где проекции вектора $ {\mathbf a}$ определены как
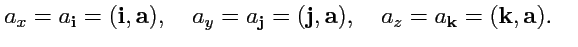$\displaystyle a_x=a_{\mathbf i}=({\mathbf i},{\mathbf a}),\quad a_y=a_{\mathbf ... ...\mathbf j},{\mathbf a}),\quad a_z=a_{\mathbf k}=({\mathbf k},{\mathbf a}).\quad$ (2)
Если орты декартовой системы координат связаны между собой следующими соотношениями
$\displaystyle [{\mathbf i},{\mathbf j}]={\mathbf k},\quad [{\mathbf j},{\mathbf k}]={\mathbf i},\quad [{\mathbf k},{\mathbf i}]={\mathbf j},\quad$ (3)
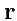
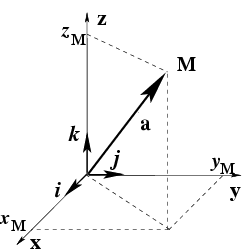
то такая система координат называется правой. В заданной декартовой системе координат для каждой точки пространства можно ввести так называемый радиус-вектор $ {\mathbf r}$ - направленный отрезок, начинающийся в начале координат и заканчивающийся в данной точке. Координаты радиус-вектора совпадают с декартовыми координатами соответствующей точки (рис. 10):
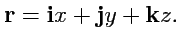$\displaystyle {\mathbf r} = {\mathbf i}x + {\mathbf j}y + {\mathbf k}z.$ (4)

Рис.10. К определению радиус-вектора

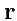
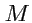
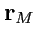
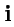
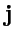
Модуль радиус-вектора $ {\mathbf r}$ равен расстоянию от начала координат до точки. Отметим следующее. Вектор $ {\mathbf a}$ как направленный отрезок не зависит от системы координат, от выбранного базиса зависят его координаты. Радиус-вектор точки $ M$ - $ {\mathbf r}_M$ "привязан" к системе координат и зависит от выбора начала координат. 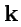Отметим также, что три орта $ {\mathbf i}$, $ {\mathbf j}$, $ {\mathbf k}$ декартовой системы координат и определяемые ими координатные оси полностью эквивалентны. Выражения (1)-(4) аналогичны для каждого орта. Поэтому, для сокращения записи введем следующие обозначения:
\begin{displaymath}\begin{array}{ccc} {\mathbf i}\equiv{\mathbf e}_1 & x \equiv ... ...bf e}_3 & z \equiv x_3 & a_z \equiv a_3. \\ [0.5em] \end{array}\end{displaymath} (5)

Тогда, декартов базис - это тройка векторов
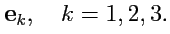$\displaystyle {\mathbf e}_k,\quad k=1,2,3.$ (6)
Координаты вектора $ {\mathbf a}$ запишутся как:
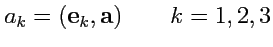$\displaystyle a_k = ({\mathbf e}_k,{\mathbf a})\qquad k=1,2,3$ (7)
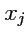
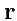
и т. д. В дальнейшем будет рассматриваться только трехмерное пространство, поэтому, если специально не указано, то индексы будут принимать значения 1, 2, 3. Например, $ x_j$ - это какая-то из трех координат радиус-вектора $ {\mathbf r}$, как принято в (5).

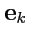
      В новых обозначениях разложение вектора $ {\mathbf a}$ по декартовому базису $ {\mathbf e}_k$ запишется как
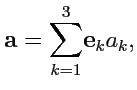$\displaystyle {\mathbf a} = \displaystyle{\sum\limits_{k=1}^{3}}{\mathbf e}_k a_k,$ (8)
а радиус-вектора
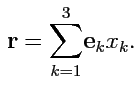$\displaystyle {\mathbf a} = \displaystyle{\sum\limits_{k=1}^{3}}{\mathbf e}_k x_k.$ (9)
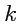
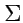
В этих выражениях индексы $ k$ уже не свободны, это индексы суммирования и от них правая часть не зависит (их можно обозначить как угодно), что видно по левой части, где находится вектор. Это соответствие будет выполняться всегда и поэтому нет необходимости писать знак суммы $ \Sigma$, а для таких выражений принято правило суммирования Эйнштейна: если выражение с индексами содержит парные индексы, то по ним предполагается суммирование (в 3-х мерном пространстве значения индексов изменяются от 1 до 3). 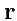Тогда, разложения вектора $ {\mathbf a}$ (8) и радиус-вектора $ {\mathbf r}$ (9) запишутся в сокращенной форме как
$\displaystyle {\mathbf a} = {\mathbf e}_i a_i,\qquad\qquad {\mathbf r} = {\mathbf e}_i x_i.$ (10)
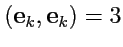
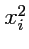
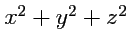
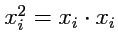
При использовании этого правила следует следить, чтобы количество свободных индексов в правой и левой частях выражения было одинаковым и не менялось при выполнении каких-либо преобразований. Например, из (1) следует, что $ ({\mathbf e}_k,{\mathbf e}_k)=3$. Иногда индекс суммирования может быть свернут арифметическим действием. Так, $ x_i^2$ следует понимать как $ x^2+y^2+z^2$, так как $ x_i^2=x_i\cdot x_i$.
Введение Скалярные и векторные поля
Векторный базис   Содержание   Дельта-символ Кронекера