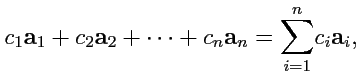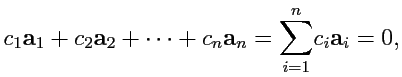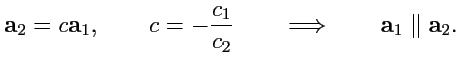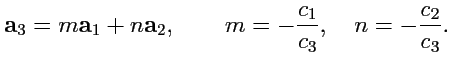1. Основные сведения из векторной алгебры
 1.5. Векторный базис
1.5. Векторный базис 
Линейной комбинацией векторов
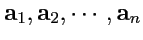
называется выражение
вида:
где
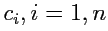
- произвольные вещественные числа.
Векторы
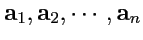
называются
линейно зависимыми, если найдутся
числа
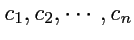
, не все равные нулю, такие, что
т. е. если существует линейная комбинация, обращающаяся в нуль. В противном случае, векторы
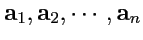
называются
линейно независимыми. Линейное пространство называется

-мерным, если в нем существует

линейно независимых векторов,
а любые
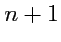
уже являются линейно зависимыми.При определении векторов, как направленных отрезков, неявно подразумевалось, что они заданы в
трехмерном евклидовом пространстве. Докажем для них несколько очевидных утверждений.
Два линейно зависимых вектора - коллинеарны. Действительно, пусть
причем (для определенности)
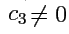
. Тогда,
Три линейно зависимых вектора - компланарны. Действительно, пусть
и по крайней мере
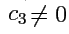
. Тогда,
Значит, вектор
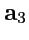
лежит в одной плоскости с векторами
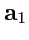
и
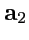
.
Если векторы

и

линейно независимы, то любой вектор
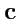
, компланарный
с ними, может быть единственным образом разложен по этим векторам, т. е. представлен в виде
их линейной комбинации
Докажем возможность такого разложения. Из условия компланарности

,

,
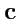
следует, что эти векторы линейно зависимы
а так как

и

линейно независимы, то
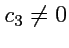
. Тогда, обозначая
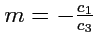
,
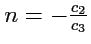
, получим искомое разложение. Докажем единственность
разложения. Пусть существует другое разложение вектора
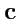
:
Тогда
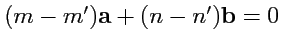
, а поскольку

и

линейно независимы, то
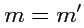
и
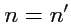
. Аналогично можно доказать третье утверждение: если три вектора

,

,
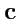
линейно зависимы (некомпланарны), то любой вектор
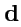
единственным образом представляется
в виде линейной комбинации
Отсюда следует, что любые четыре вектора в трехмерном пространстве являются линейно зависимыми.
Базисом в трехмерном пространстве называется тройка векторов
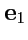
,
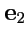
,
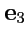
, таких, что любой вектор

может быть однозначно представлен в виде
линейной комбинации этих векторов:
Коэффициенты
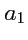
,
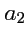
,
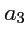
называют
координатами (компонентами) вектора

в
базисе
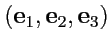
. Очевидно, что базисов может быть сколь угодно много - любые три некомпланарных вектора можно
выбрать в качестве базиса.