1. Основные сведения из векторной алгебры
 1.4. Векторное и смешанное произведение векторов
1.4. Векторное и смешанное произведение векторов 
Наряду со скалярным произведением, сопоставляющим двумвекторам число, для векторов можно
ввести и так называемое векторное произведение, которое сопоставляет двум векторам новый
вектор.
Векторным произведением векторов

и

называется вектор
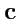
,
обозначаемый как
![$ {\mathbf c}=[{\mathbf a},{\mathbf b}]$](img77.png)
(или
![$ [{\mathbf a}\times{\mathbf b}]$](img78.png)
,
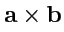
),
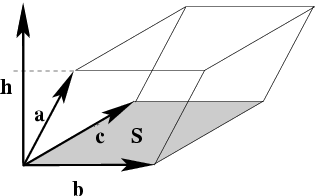
модуль которого равен площади параллелограмма, построенного на векторах

и

,
отложенных из одной точки, а направление совпадает с поступательным движением
правого винта (
рис.7).
Рис.7. К определению векторного произведения векторов.
Легко видеть, что
В отличие от скалярного произведения, векторное является
антикоммутативным, т. е.
![$ [{\mathbf a},{\mathbf b}]=-[{\mathbf b},{\mathbf a}]$](img82.png)
, но,
как и скалярное произведение, оно обладает свойством
дистрибутивности:
![$ [{\mathbf a},{\mathbf b}+{\mathbf c}]=[{\mathbf a},{\mathbf b}]+[{\mathbf a},{\mathbf c}]$](img83.png)
.
Скалярное произведение векторов

и
![$ {\mathbf d}=[{\mathbf b},{\mathbf c}]$](img84.png)
, т. е
![$ ({\mathbf a},[{\mathbf b},{\mathbf c}])$](img85.png)
называется
смешанным произведением трех векторов. По определению скалярного произведения
и ясно, что смешанное произведение по модулую равно объему параллелепипеда, построенного на
векторах

,

,
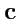
(
рис.8)
Рис.8. К определению смешанного произведения векторов.
Отсюда следует, что если три вектора
являются компланарными, то их смешанное произведение равно нулю. В смешанном произведении
сомножители можно переставлять местами циклически:
Рассмотрим векторное произведение вектора

на векторное произведение
![$ [{\mathbf b},{\mathbf c}]$](img88.png)
,
т. е. построим вектор
![$ {\mathbf d}=[{\mathbf a},[{\mathbf b},{\mathbf c}]]$](img89.png)
. Полученное произведение называется
двойным векторным произведением. Результирующий вектор
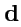
по определению векторного
произведения перпендикулярен векторам
![$ [{\mathbf b},{\mathbf c}]$](img88.png)
и

, т. е.
![$ ({\mathbf d},[{\mathbf b},{\mathbf c}])=0$](img91.png)
и
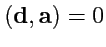
. Но, если смешанное произведение равно нулю,
то векторы, которые в него входят, являются компланарными и, как будет показано ниже, вектор
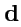
можно представить в виде
Тогда,
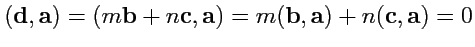
, откуда
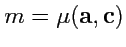
,
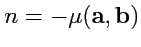
, после чего оказывается, что
![$ {\mathbf d}=[{\mathbf a},[{\mathbf b},{\mathbf c}]]=\mu\{({\mathbf a},{\mathbf c}){\mathbf b} - ({\mathbf a},{\mathbf b}){\mathbf c} \}$](img97.png)
. Можно
показать, что коэффициент
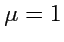
и тогда получается правило раскрытия двойного векторного
произведения, которое для удобства запоминания записывается в форме:
![$\displaystyle [{\mathbf a},[{\mathbf b},{\mathbf c}]]={\mathbf b}({\mathbf a},{\mathbf c}) - {\mathbf c}({\mathbf a},{\mathbf b})$](img99.png)
(правило БАЦ минус ЦАБ).
Как следствие из последней формулы, можно произвести разложение произвольного вектора

по двум направлениям, параллельному и перпендикулярному данному вектору

:
Это разложение автоматически получается из формулы для двойного векторного произведения, если
если в ней положить
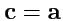
.
Заметим, что двойное векторное произведение не обладает свойством ассоциативности :
![$ [{\mathbf a},[{\mathbf b},{\mathbf c}]]\ne[[{\mathbf a},{\mathbf b}],{\mathbf c}]$](img102.png)
.
И наконец, последнее в этом разделе. Получаемый в результате векторного произведения вектор,
вообще говоря, истинным вектором не является. Он по своей внутренней структуре отличается
от обычных векторов (задание его направления зависит от "винта": для правого оно одно, для левого
оно противоположное). По этой же причине смешанное произведение не является истинным скаляром.
Чтобы подчеркнуть указанное отличие, обычные векторы иногда называют полярными, а векторы,
связанные с векторным произведением, аксиальными или псевдовекторами. Более детально все различия между векторами и псевдовекторами будут рассмотрены позже.
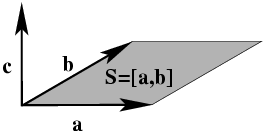
![$\displaystyle c = \vert[{\mathbf a},{\mathbf b}]\vert = a\ b\sin\widehat{({\mathbf a},{\mathbf b})}.
$](img80.png)
![$\displaystyle ({\mathbf a},[{\mathbf b},{\mathbf c}]) = a\vert[{\mathbf b},{\ma...
...
\vert[{\mathbf b},{\mathbf c}]\vert\ a_{\vert[{\mathbf b},{\mathbf c}]\vert},
$](img86.png)
![$\displaystyle {\mathbf b}={\mathbf b}' + {\mathbf b}'',\quad
{\mathbf a}\uparro...
...hbf b}'' = \displaystyle{\frac{[{\mathbf a},[{\mathbf b},{\mathbf a}]]}{a^2}}.
$](img100.png)